搜索
【题目】如图，已知
， 
， 
，试说明：BE∥CF．
完善下面的解答过程，并填写理由或数学式：
解：∵ 
（已知）
∴AE∥ （ ）
∴
（ ）
∵
（已知）
∴
（ ）
∴DC∥AB（ ）
∴
（ ）
即
∵
（已知）
∴
（ ）
即
∴BE∥CF（ ） ．
参考答案：
【答案】答案见解析．
【解析】试题分析：根据平行线的判定与性质，灵活判断同位角、内错角、同旁内角，逐步可求解.
试题解析：解：∵
（已知）
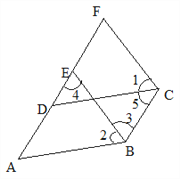
∴AE∥ BC （ 内错角相等，两直线平行）
∴
（ 两直线平行，内错角相等）
∵
（已知）
∴
（ 等量代换）
∴DC∥AB （ 同位角相等，两直线平行）
∴
（ 两直线平行，同旁内角互补）
即
∵
（已知）
∴
（ 等量代换 ）
即
∴BE∥CF （ 同旁内角互补，两直线平行 ） ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校八年级在一次广播操比赛中，三个班的各项得分如下表：
服装统一
动作整齐
动作准确
八（1）班
80
84
87
八（2）班
97
78
80
八（3）班
90
78
85
(1) 填空：根据表中提供的信息，在服装统一方面，三个班得分的平均数是_________；在动作准确方面最有优势的是_________班
(2) 如果服装统一、动作整齐、动作准确三个方面按20%、30%、50%的比例计算各班的得分，请通过计算说明哪个班的得分最高
-
科目： 来源： 题型：
查看答案和解析>>【题目】（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】某家电销售商场电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等．
（1）求每台电冰箱与空调的进价分别是多少？
（2）现在商场准备一次购进这两种家电共100台，设购进电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13200元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
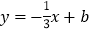与x轴交于点A，与y轴交于点B，与直线y＝x交于点E，点E的横坐标为3(1) 求点A的坐标
(2) 在x轴上有一点P（m，0），过点P作x轴的垂线，与直线
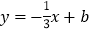交于点C，与直线y＝x 交于点D．若CD≥4，则m的取值范围为___________________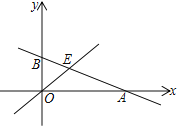
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A，B分别为数轴上的两点，点A表示的数是﹣30，点B表示的数是50．
（1）请写出线段AB中点M表示的数是 ．
（2）现有一只蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左移动，同时另一只蚂蚁Q恰好从点A出发，以每秒2个单位长度的速度沿数轴向右移动，设两只蚂蚁在数轴上的点C相遇．
①求A、B两点间的距离；
②求两只蚂蚁在数轴上的点C相遇时所用的时间；
③求点C对应的数是多少？
（3）若蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左运动，同时另一只蚂蚁恰好从A点出发，以每秒2个单位长度的速度沿数轴也向左运动，设两只蚂蚁在数轴上的D点相遇，求D点表示的数是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O是直线AB上一点，OD平分∠AOC．
（1）若∠AOC=60°，请求出∠AOD和∠BOC的度数.
（2）若∠AOD和∠DOE互余，且∠AOD=
∠AOE，请求出∠AOD和∠COE的度数．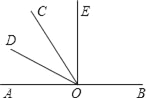
相关试题
