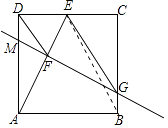
【题目】如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF= ![]() ,②DF∥EG,③△EFG≌△ECG,④BG=
,②DF∥EG,③△EFG≌△ECG,④BG= ![]() ,正确的有:(填写序号)
,正确的有:(填写序号)
参考答案:
【答案】①④
【解析】解:如图,设FG交AD于M,连接BE.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ADC=∠C=90°,
∵DE=EC=2,
在Rt△ADE中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
∵AF=EF,
∴DF= ![]() AE=
AE= ![]() ,故①正确,
,故①正确,
易证△AED≌△BEC,
∴∠AED=∠BEC,
∵DF=EF,
∴∠FDE=∠FED=∠BEC,
∴DF∥BE,
∵BE与EG相交,
∴DF与EG不平行,故②错误,
∵AE⊥MG,易证AE=MG=2 ![]() ,
,
由△AFM∽△ADE,可知 ![]() =
= ![]() ,
,
∴FM= ![]() ,FG=
,FG= ![]() ,
,
在Rt△EFG中,EG= ![]() =
= ![]() ,
,
在Rt△ECG中,CG= ![]() =
= ![]() ,
,
∴BG=BC﹣CG=4﹣ ![]() =
= ![]() ,故④正确,
,故④正确,
∵EF≠EC,FG≠CG,∴△EGF与△EGC不全等,故③错误,
所以答案是①④.
【考点精析】利用线段垂直平分线的性质和正方形的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
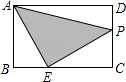
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是
( )
A.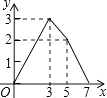
B.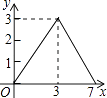
C.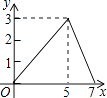
D.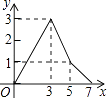
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:
 (1)本次接受问卷调查的同学有多少人?补全条形统计图.
(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE=CF.
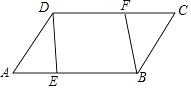
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
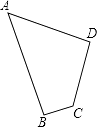
(1)判断∠D是否是直角,并说明理由.
(2)求四边形草坪ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3﹣ab2= .
相关试题

