搜索
【题目】小明的家在某公寓楼AD内，他家的前面新建了一座大厦BC，小明想知道大厦的高度，但由于施工原因，无法测出公寓底部A与大厦底部C的直线距离，于是小明在他家的楼底A处测得大厦顶部B的仰角为60°，爬上楼顶D处测得大厦的顶部B的仰角为30°，已知公寓楼AD的高为60米，请你帮助小明计算出大厦的高度BC．
参考答案：
【答案】大厦的高度BC为90米．
【解析】试题分析：在图中有两个直角三角形，即
和
若设
则根据30°、60°角的正切值可求得BC和BE，然后根据二者之间的关系，得到一个关于
的方程解答即可．
试题解析：如图，由题意知：四边形ACED是矩形，
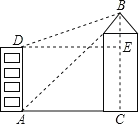
∴AC=DE,DA=EC=60米, 
设DE=x，
在Rt△BDE中，
在Rt△BAC中，
即
解得： 
(米).
答：大厦的高度BC为90米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，过点A作⊙O的切线，交OC的延长线于点D，∠D=30°
（1）求∠B的度数；
（2）若OD⊥AB，BC=5，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（0，4），C（﹣3，2）．
（1）如图，求△ABC的面积．
（2）若点P的坐标为（m，0），
①请直接写出线段AP的长为______（用含m的式子表示）；
②当S△PAB=2S△ABC时，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质一运用函数解决问题“的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义|a|＝
．结合上面经历的学习过程，现在来解决下面的问题：在函数y＝|kx﹣1|+b中，当x＝1时，y＝3，当x＝0时，y＝4．
（1）求这个函数的表达式；
（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象；
（3）已知函数y＝
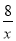的图象如图所示，结合你所画的函数图象，直接写出不等式|kx﹣1|+b≥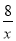的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：
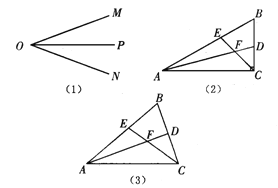
（1）如图（2），在△ABC中，∠ACB是直角，∠B＝60°， AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系；
（2）如图（3），在△ABC中，如果∠ACB不是直角，而（1）中的其他条件不变，在（1）中所得结论是否仍然成立？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c（a≠0）与x轴交于不同的两个点A（x1，0）和点B（x2，0）与y轴的正半轴交于点C，如果x1，x2是方程x2﹣2x﹣3=0的两个根（x1＜x2），且图象经过点（2，3）
（1）求抛物线的解析式并画出图象
（2）x在什么范围内函数值y大于3且随x的增大而增大．
（3）设（1）中的抛物线顶点为D，在y轴上是否存在点P，使得DP+BP的和最小？若存在，求出这个最小值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将分别标有数字2,3,5的三张颜色、质地、大小完全一样的卡片背面朝上放在桌面上.
（1）随机抽取一张,求抽到奇数的概率；
（2）随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并画树状图或列表求出抽取到的两位数恰好是35的概率.
相关试题
