【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
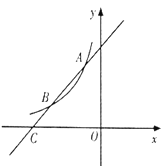
(1)求此反比例函数的表达式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)反比例函数的表达式为![]() ;(2)点P(-6,0)或(-2,0).
;(2)点P(-6,0)或(-2,0).
【解析】(1)把点A(-1,a)代入![]() ,得
,得![]() ,得到A(-1,3),
,得到A(-1,3),
代入反比例函数![]() ,得
,得![]() ,即可求得反比例函数的表达式.
,即可求得反比例函数的表达式.
(2)联立两个函数表达式得 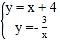 ,解得
,解得 ![]() ,
,![]() .求得点B的坐标,
.求得点B的坐标,
当![]() 时,得
时,得![]() .求得点C(-4,0). 设点P的坐标为(
.求得点C(-4,0). 设点P的坐标为(![]() ,0).根据
,0).根据![]() ,列出方程求解即可.
,列出方程求解即可.
【解答】(1)把点A(-1,a)代入![]() ,得
,得![]() ,
,
∴ A(-1,3)
把A(-1,3)代入反比例函数![]() ,得
,得![]() ,
,
∴ 反比例函数的表达式为![]() .
.
(2)联立两个函数表达式得 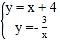 ,解得
,解得 ![]() ,
,![]() .
.
∴ 点B的坐标为B(-3,1).
当![]() 时,得
时,得![]() .
.
∴ 点C(-4,0).
设点P的坐标为(![]() ,0).
,0).
![]() ,
,
∴ ![]() .
.
即 ![]() ,
,
解得 ![]() ,
,![]() .
.
∴ 点P(-6,0)或(-2,0).
-
科目: 来源: 题型:
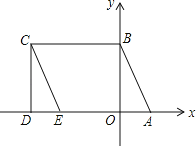
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=
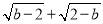 ﹣3.
﹣3.(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
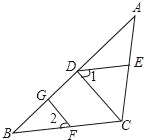
查看答案和解析>>【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
-
科目: 来源: 题型:
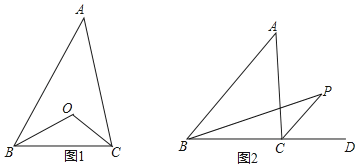
查看答案和解析>>【题目】(1)如图1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度数;
(2)如图2,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,先写出∠A和∠P的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
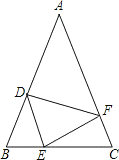
(1)求证:DE=EF;
(2)当∠A=44°时,求∠DEF的度数;
(3)当∠A等于多少度时,△DEF成为等边三角形?试证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
 .
.(1)点A的坐标为 ;点B的坐标为 ;
(2)如图1,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
(3)如图2,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P 作PG⊥BM,交AN的延长线于点G,请写出线段AG、OP与PG之间的数量关系,并证明你的结论.

相关试题

