【题目】如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足![]() .
.
(1)点A的坐标为 ;点B的坐标为 ;
(2)如图1,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
(3)如图2,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P 作PG⊥BM,交AN的延长线于点G,请写出线段AG、OP与PG之间的数量关系,并证明你的结论.

参考答案:
【答案】(1) A(5,0) ,B(0,-5) ;(2)D(2,3);(3) OP+PG=AG.
【解析】试题分析:(1)根据非负数的性质得出a=5,b=﹣5即可;
(2)过C作CK⊥x轴,过D作CF⊥y轴,再利用AAS证明△AOC与△DOB全等即可;
(3)延长GP到L使PL=OP,连接AL,证明△PAL与△OAP全等,再利用全等三角形的性质解答即可.
试题解析:解:(1)∵|a+b|+(a﹣5)2=0,∴a=5,b=﹣5,∴点A的坐标为(5,0),点B的坐标为(0,﹣5),故答案为:(5,0);(0,﹣5);
(2)过C作CK⊥x轴,过D作DF⊥y轴,∵∠AED=∠BOK=90°,∴∠DBO=∠OAC,∵∠AOB+BOC=∠BOK+∠BOC=90°+∠BOC,∴∠AOC=∠BOD,在△AOC与△DOB中,∵∠AOC=∠BOD,∠DBO=∠OAC,OA=OB,∴△AOC≌△DOB(AAS),∴OC=OD,在△OCK与△ODF中,∵∠DFO=∠CKO=90°,∠DOF=∠COK,OD=OC,∴△OCK≌△ODF,∴DF=CK,OK=OF,∴D(﹣2,3);
(3)延长GP到L,使PL=OP,连接AL,在△AON与△BOM中,∵ON=OM,∠AON=∠BOM,OA=OB,∴△AON≌△BOM,∴∠OAN=∠OBM,∴∠MBA=∠NAB,∵PG⊥BM,OP⊥AN,∴∠NAB+∠OPA=∠MBA+∠GPB=90°,∴∠OPA=∠GPB=∠APL,在△OAP与△PAL中,∵PL=OP,∠APL=∠OPA,AP=AP,∴△OAP≌△PAL,∴∠POA=∠L,∠OAP=∠PAL=45°,∴∠OAL=90°,∴∠POA=90°﹣∠POB,∠GAL=90°﹣∠OAN,∵∠POB=∠OAN,∴∠POA=∠GOL,∴∠POA=∠GOL=∠L,∴AG=GL,∴AG=GL=GP+PL=GP+OP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市有一块长为(3a+b) 米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=10,b=8,且每平方米造价为100元求出绿化需要多少费用.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=
 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
A.
 B. 3 C. 2 D. 2
B. 3 C. 2 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图点P为△ABC的外角∠BCD的平分线上一点,PA=PB.
(1)如图1,求证:∠PAC=∠PBC;
(2)如图2,作PE⊥BC于E,若AC=5,BC=11,则
 = ;
= ;(3)如图3,若M、N分别是边AC、BC上的点,且∠MPN=
 ∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.
∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
据林业专家分析,树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同,求一片国槐树叶一年的平均滞尘量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你阅读下列计算过程,再回答所提出的问题:
题目计算

解:原式=
 (A)
(A)=
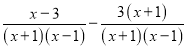 (B)
(B)=x-3-3(x+1) (C)
=-2x-6 (D)
(1)上述计算过程中,从哪一步开始出现错误:_______________
(2)如果假设基于之前步骤正确的前提下,从B到C是否正确,若不正确,错误的原因是____________________________________________________
(3)请你正确解答。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为__.

相关试题

