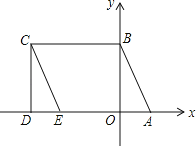
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() ﹣3.
﹣3.
(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
参考答案:
【答案】(1)(-3,2);(2)(-2,0);(3)x+y=z,见解析
【解析】
(1)直接利用二次根式的性质得出a,b的值,即可得出答案;
(2)利用平移的性质得出点E的坐标;
(3)利用平行线的性质分析得出答案.
(1)∵a=![]() +
+![]() ﹣3,
﹣3,
∴b=2,a=﹣3,
∵点C的坐标为(a,b),
∴点C的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)∵点B在y轴上,点C的坐标为:(﹣3,2),
∴B点向左平移了3个单位长度,
∴A(1,0),向左平移3个单位得到:(﹣2,0)
∴点E的坐标为:(﹣2,0);
故答案为:(﹣2,0);
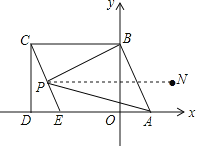
(3)x+y=z.证明如下:
如图,过点P作PN∥CD,
∴∠CBP=∠BPN
又∵BC∥AE,
∴PN∥AE
∴∠EAP=∠APN
∴∠CBP+∠EAP=∠BPN+∠APN=∠APB,
即x+y=z.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在平面直角坐标系中点A(a,b)点B(a,0),且满足|2a-b|+(b-4)2=0.
(1)求点A、点B的坐标;
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动.同时点Q从C点出发,沿y轴负方向以2个单位每秒的速度移动,某一时刻,如图所示且S阴=
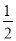 S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;(3)在(2)的条件下,AQ交x轴于M,作∠ACO,∠AMB的角平分线交于点N,判断
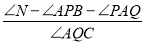 是否
是否 为定值,若是定值求其值;若不是定值,说明理由.
为定值,若是定值求其值;若不是定值,说明理由.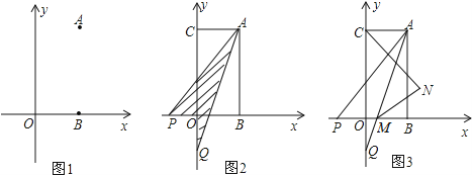
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACB的平分线交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
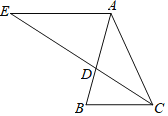
(1)求∠ADC的度数;
(2)求证:AE=AC
(3)试问△ADE是等腰三角形吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列计算过程,猜想立方根.
 =1
=1 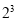 =8
=8  =27
=27 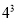 =64
=64  =125
=125 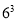 =216
=216 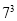 =343
=343 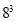 =512
=512 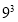 =729
=729 (1)小明是这样试求出19683的立方根的,先估计19683的立方根的个位数, 猜想它的个位数为 , 又由
 <19000<
<19000< 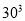 ,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
,猜想19683的立方根十位数为 ,验证得19683的立方根是 .(2)请你根据(1)中小明的方法,完成如下填空:
①
 = ; ②
= ; ②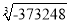 = ;③
= ;③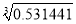 = .
= . -
科目: 来源: 题型:
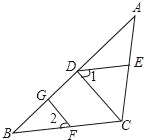
查看答案和解析>>【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度数;
(2)如图2,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,先写出∠A和∠P的数量关系,并证明你的结论.
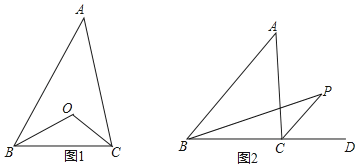
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
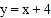 的图象与反比例函数
的图象与反比例函数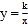 (
(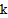 为常数且
为常数且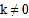 )的图象交于
)的图象交于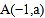 ,
, 两点,与
两点,与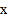 轴交于点
轴交于点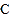 .
.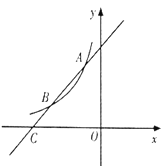
(1)求此反比例函数的表达式;
(2)若点
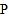 在
在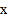 轴上,且
轴上,且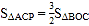 ,求点
,求点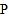 的坐标.
的坐标.
相关试题

