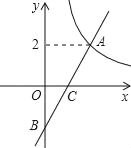
【题目】已知,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.
参考答案:
【答案】(1)y=2x﹣2;(2)P点坐标为(4,0),(﹣2,0).
【解析】
(1)将A点坐标代入y=![]() (x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式;
(x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式;
(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加.
解:(1)根据题意,将点A(m,2)代入y=![]() ,
,
得:2=![]() ,
,
解得:m=2,
即点A(2,2),
将点A(2,2)代入y=kx﹣k,得:2=2k﹣k,
解得:k=2,
∴一次函数的解析式为y=2x﹣2;
(2)如图,
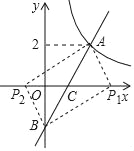
∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为B(0,﹣2),
S△ABP=S△ACP+S△BPC,
∴![]() ×2CP+
×2CP+![]() ×2CP=6,
×2CP=6,
解得CP=3,
则P点坐标为(4,0),(﹣2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位),1个大桶加上5个小桶可以盛酒2斛。
(1)1个大桶、1个小桶分别可以盛酒多少斛?
(2)盛酒16斛,需要大桶、小桶各多少?(写出两种方案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

-
科目: 来源: 题型:
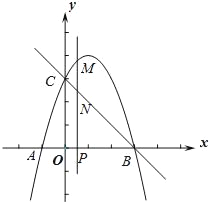
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
-
科目: 来源: 题型:
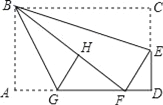
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=
 S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.其中正确的是__.(把所有正确结论的序号都选上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
相关试题

