【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,-1)、B(2,0)、C(0,3),AC交![]() 轴于点D,AB交
轴于点D,AB交![]() 轴于点E.
轴于点E.
(1)△ABC的面积为________;
(2)点E的坐标为________;
(3)若点P的坐标为(0,![]() ):
):
①线段EP的长为________(用含![]() 的式子表示);
的式子表示);
②当![]() 时,求点P的坐标。
时,求点P的坐标。

参考答案:
【答案】(1)面积为7;(2)E(0,-0.5);(3)①![]() ;②P(0,6.5),(0,-7.5).
;②P(0,6.5),(0,-7.5).
【解析】
(1)根据已知条件得到直线AC的解析式为y=2x+3,即可得到D(-![]() ,0),根据三角形的面积公式即可得到结论;
,0),根据三角形的面积公式即可得到结论;
(2)根据已知条件得到直线AB的解析式为y=![]() x-
x-![]() ,于是得到结论;
,于是得到结论;
(3)①根据点的坐标求得线段EP的长|-![]() -m|=|
-m|=|![]() +m|;
+m|;
②根据三角形的面积公式列方程即可得到结论.
解:(1)∵A(-2,-1)、C(0,3),
∴直线AC的解析式为y=2x+3,
∴当y=0时,x=-![]() ,
,
∴D(-![]() ,0),
,0),
∴△ABC的面积=![]() ×(2+
×(2+![]() )×(3+1)=7;
)×(3+1)=7;
(2)∵A(-2,-1)、B(2,0),
∴设直线AB的解析式为:y=kx+b,
∴![]() ,
,
∴ ,
,
∴y=![]() x-
x-![]() ,
,
∴E(0,-0.5);
(3)①∵点P的坐标为(0,m),
∴线段EP的长|-![]() -m|=|
-m|=|![]() +m|;
+m|;
②∵S△PAB=2S△ABC,
∴![]() ×|
×|![]() +m|×(2+2)=2×7,
+m|×(2+2)=2×7,
∴m=6.5或m=-7.5.
∴点P的坐标为:(0,6.5)或(0,-7.5)
-
科目: 来源: 题型:
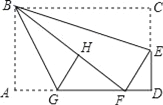
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=
 S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.其中正确的是__.(把所有正确结论的序号都选上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了配合足球进校园的活动,实验学校在体育用品专卖店购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。求购买一个甲种足球,一个乙种足球各需多少元?
-
科目: 来源: 题型:
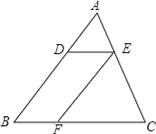
查看答案和解析>>【题目】如图,在△ABC中,DE∥BC,EF∥AB,若S△ADE=4cm2,S△EFC=9cm2,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一
A:计时制:0.05元/分,B:包月制:50元/月,此外,每一种上网时间都要收通信费0.02元/分
(1)某用户某月上网时间为x小时,请写出两种收费方式下该用户应该支付的费用(用y表示)
(2)若甲用户估计一个月上网时间为20小时,乙用户估计一个月上网时间为15小时,各选哪一种收费方式最合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程
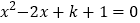 有两个不相等的实数根x1,x2.
有两个不相等的实数根x1,x2. (1)求k的取值范围;
(2)如果
 ,且k为整数,求k的值.
,且k为整数,求k的值.
相关试题

