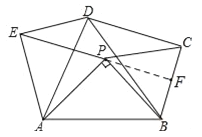
【题目】如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是 .

参考答案:
【答案】1.
【解析】
试题分析:延长EP交BC于点F,∵∠APB=90°,∠AOE=∠BPC=60°,∴∠EPC=150°,∴∠CPF=180°﹣150°=30°,∴PF平分∠BPC,又∵PB=PC,∴PF⊥BC,设Rt△ABP中,AP=a,BP=b,则
CF=![]() CP=
CP=![]() b,
b,![]() ,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×
,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×![]() b=
b=![]() ab,又∵
ab,又∵![]() ≥0,∴2ab≤
≥0,∴2ab≤![]() ,∴
,∴![]() ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.
ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解x3-2x2+x正确的是( )
A. (x-1)2 B. x(x-1)2 C. x(x2-2x+1) D. x(x+1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF. 求证:
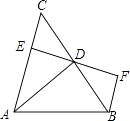
(1)AB=AC;
(2)BC平分∠ABF. -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。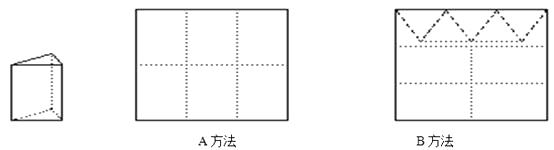
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,另一边ON仍在直线AB的下方.
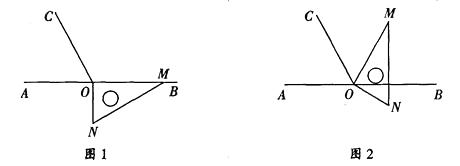
(1)若OM恰好平分∠BOC,求∠BON的度数;
(2)若∠BOM等于∠COM余角的3倍,求∠BOM的度数;
(3)若设∠BON=α(0°<α<90°),试用含α的代数式表示∠COM. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:(2x+y)2﹣(x+2y)2 .
-
科目: 来源: 题型:
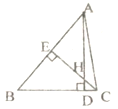
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB.
相关试题

