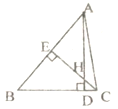
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB.
参考答案:
【答案】答案不唯一,如:AH=CB或EH=EB或AE=CE.
【解析】
试题分析:∵AD⊥BC,CE⊥AB,垂足分别为D、E,∴∠BEC=∠AEC=90°,在Rt△AEH中,∠EAH=90°﹣∠AHE,又∵∠EAH=∠BAD,∴∠BAD=90°﹣∠AHE,在Rt△AEH和Rt△CDH中,∠CHD=∠AHE,∴∠EAH=∠DCH,∴∠EAH=90°﹣∠CHD=∠BCE,所以根据AAS添加AH=CB或EH=EB;
根据ASA添加AE=CE.可证△AEH≌△CEB.
故答案为:AH=CB或EH=EB或AE=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,另一边ON仍在直线AB的下方.
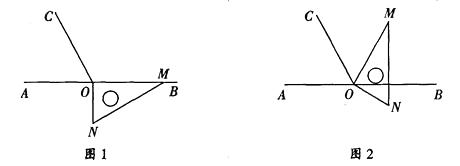
(1)若OM恰好平分∠BOC,求∠BON的度数;
(2)若∠BOM等于∠COM余角的3倍,求∠BOM的度数;
(3)若设∠BON=α(0°<α<90°),试用含α的代数式表示∠COM. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:(2x+y)2﹣(x+2y)2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式成立的是( ).
A.(a2)3=a6
B.2a2-3a=-a
C.a6÷a3=a2
D.(a+4)(a-4)=a2-4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+3b=5ab
B.a2a3=a5
C.(2a)3=6a 3
D.a6+a3=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.

(1)把﹣16,9,16,﹣5,﹣9,5分别填入图中的六个小正方形中;
(2)若某相对两个面上的数字分别为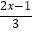 和
和 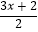 ﹣5,求x的值.
﹣5,求x的值.
相关试题

