【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
求证:DC⊥BE.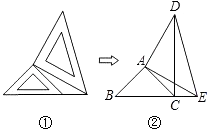
参考答案:
【答案】证明:∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD,
在△ABE和△ACD中, 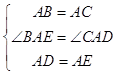 ,
,
∴△ABE≌△ACD(SAS),
∴∠ACD=∠B,
∴∠DCB=∠ACB+∠ACD=∠ACB+∠B=90°,
∴DC⊥BE.
【解析】根据等腰直角三角形的性质可得AB=AC,AE=AD,∠BAC=∠DAE=90°,再求出∠BAE=∠CAD,然后利用“边角边”证明△ABE和△ACD全等,根据全等三角形对应角相等可得∠ACD=∠B,再求出∠DCB=90°,最后根据垂直的定义证明即可.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
A.10°
B.20°
C.30°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过矩形ABCD对角线的交点O , 且分别交AB、CD于E、F , 那么阴影部分的面积与矩形ABCD面积的大小关系是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且
 =PEPO.
=PEPO.(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE=CF,AB∥CD,AB=CD.求证:AF∥DE.

-
科目: 来源: 题型:
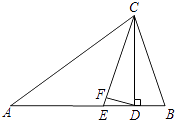
查看答案和解析>>【题目】如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)30﹣2﹣3+(﹣3)2﹣( )﹣1
)﹣1
(2)(2x﹣3y)2﹣(y+3x)(3x﹣y)
相关试题

