【题目】如图,EF过矩形ABCD对角线的交点O , 且分别交AB、CD于E、F , 那么阴影部分的面积与矩形ABCD面积的大小关系是什么?
参考答案:
【答案】解答:解:阴影部分的面积与矩形ABCD面积的 ![]() ∵四边形为矩形,∴OB=OD=OA=OC , 在△EBO与△FDO中,∠EOB=∠DOF , OB=OD , ∠EBO=∠FDO , △EBO≌△FDO , ∴S阴影部分的面积=
∵四边形为矩形,∴OB=OD=OA=OC , 在△EBO与△FDO中,∠EOB=∠DOF , OB=OD , ∠EBO=∠FDO , △EBO≌△FDO , ∴S阴影部分的面积= ![]() ,∵△AOB与△ABC同底且△AOB的高是△ABC高的
,∵△AOB与△ABC同底且△AOB的高是△ABC高的 ![]() ,∴
,∴ ![]() S矩形ABCD .
S矩形ABCD .
【解析】本题主要根据矩形的性质,得△EBO≌△FDO , 再由△AOB与△OBC同底等高,得出结论.
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a是有理数,那么-8a>-5a。()
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数的一般形式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
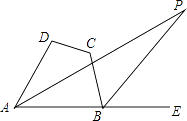
A.10°
B.20°
C.30°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且
 =PEPO.
=PEPO.(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
求证:DC⊥BE.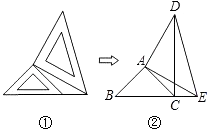
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE=CF,AB∥CD,AB=CD.求证:AF∥DE.

相关试题

