【题目】如图,已知BE=CF,AB∥CD,AB=CD.求证:AF∥DE. 
参考答案:
【答案】解:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
∵AB∥CD,
∴∠B=∠C,
在△ABF和△CDE中  ,
,
∴△ABF≌△CDE(SAS),
∴∠AFB=∠DEC,
∴AF∥DE.
【解析】首先利用等式的性质可得BF=CE,再根据平行线的性质可得∠B=∠C,然后利用SAS定理判定△ABF≌△CDE,进而可得∠AFB=∠DEC,从而可得结论.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过矩形ABCD对角线的交点O , 且分别交AB、CD于E、F , 那么阴影部分的面积与矩形ABCD面积的大小关系是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且
 =PEPO.
=PEPO.(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
求证:DC⊥BE.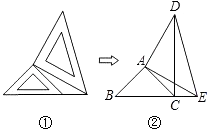
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=°.
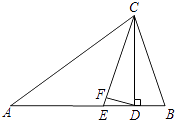
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)30﹣2﹣3+(﹣3)2﹣( )﹣1
)﹣1
(2)(2x﹣3y)2﹣(y+3x)(3x﹣y) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
 甲由于看错了方程(1)中的a,得到方程组的解为
甲由于看错了方程(1)中的a,得到方程组的解为 , 乙由于看错了方程(2)中的b,得到方程组的解为
, 乙由于看错了方程(2)中的b,得到方程组的解为 , 若按正确的计算,求x+6y的值.
, 若按正确的计算,求x+6y的值.
相关试题

