【题目】如图,在平面直角坐标系中,直线![]() 经过第一、二、三象限,与
经过第一、二、三象限,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在这条直线上,连接
在这条直线上,连接![]() ,已知
,已知![]() 的面积等于1.
的面积等于1.

(1)求![]() 的值;
的值;
(2)如果反比例函数y=![]() (k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
参考答案:
【答案】(1)1
(2)![]()
【解析】
(1) 由A的横坐标为2得到AC=2,对于直线解析式,令y=0求出x的值,表示出OB的长,三角形AOB面积以OB为底,AC为高表示出,根据已知三角形的面积求出OB的长,确定出B坐标,代入一次函数解析式中即可求出b的值;
(2)将A坐标代入一次函数求出t的值,确定出A坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式.
(1)解:∵直线![]() 经过第一、二、三象限,与
经过第一、二、三象限,与![]() 轴交于点
轴交于点![]() ,
,
∴![]()
∵![]() 的面积等于1,点
的面积等于1,点![]()
∴![]()
∴![]()
(2)由b=1,得到直线解析式为y=![]() x+1,
x+1,
将A(2,t)代入直线解析式得:t=1+1=2,即A(2,2),
把A(2,2)代入反比例解析式得:k=4,
则反比例解析式为y=![]()
即点![]() 在直线
在直线![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,
, ,
, ,
, 分别是四边形
分别是四边形 各边的中点,且
各边的中点,且 ,
, ,
, .
.
(1)试判断四边形
 的形状,并证明你的结论;
的形状,并证明你的结论;(2)如图2,依次取
 ,
, ,
, ,
, 的中点
的中点 ,
, ,
, ,
, ,再依次取
,再依次取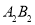 ,
, ,
, ,
, 的中点
的中点 ,
, ,
, ,
, ……以此类推,取
……以此类推,取 ,
, ,
,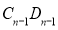 ,
, 的中点
的中点 ,
, ,
, ,
, ,根据信息填空:
,根据信息填空:①四边形
 的面积是__________;
的面积是__________;②若四边形
 的面积为
的面积为 ,则
,则 ________;
________;③试用
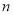 表示四边形
表示四边形 的面积___________.
的面积___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )

①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;
②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;
③每人乘坐地铁的月均花费的中位数在60~100元范围内;
④乘坐地铁的月均花费达到80元以上的人可以享受折扣.
A.①②④B.①③④C.③④D.①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校带领学生演出,参加演出的女生人数是男生人数的2倍少100人,学校需要采购一批演出服装.经了解:
 两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商:
两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商: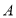 公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费;
公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费; 公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有
公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有 人.
人.(1)分别写出学校购买
 两公司服装所付的总费用
两公司服装所付的总费用 (元)和
(元)和 (元)与参演男生人数
(元)与参演男生人数 (人)之间的函数关系式;
(人)之间的函数关系式;(2)当参演男生人数是100人时,学校选用哪家制衣公司合算?当参演男生人数是300人时,学校选用哪家制衣公司合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )

A. 50m B. 100m C. 160m D. 200m
-
科目: 来源: 题型:
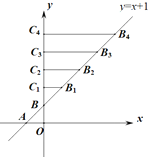
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作y 轴的垂线,垂足为点C1,得到⊿BB1C1;在直线 AB上截取B1B2= BB1,过点B2分别作y 轴的垂线,垂足为点C2,得到⊿BB2C2;在直线AB上截取B2B3= B1B2,过点B3作y 轴的垂线,垂足为点C3,得到⊿BB3C3;……;第3个⊿BB3C3的面积是___________;第n个⊿BBnCn的面积是______________(用含n的式子表示,n是正整数).
相关试题

