搜索
【题目】计算： 
﹣4 
﹣tan60°+| 
﹣2|．
参考答案：
【答案】解：原式=2 
﹣4× 
﹣ +2﹣
=2﹣2 
【解析】根据二次根式的化简技巧将二次根式化简，同时根据绝对值的意义去掉绝对值符号，并代入特殊锐角的三角函数值，然后按照实数的运算法则运算即可。
【考点精析】解答此题的关键在于理解二次根式的性质与化简的相关知识，掌握1、如果被开方数是分数（包括小数）或分式，先利用商的算数平方根的性质把它写成分式的形式，然后利用分母有理化进行化简．2、如果被开方数是整数或整式，先将他们分解因数或因式，然后把能开得尽方的因数或因式开出来，以及对绝对值的理解，了解正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠BOP与OP上点C，点A(在A的左侧)，嘉嘉进行如下作图：
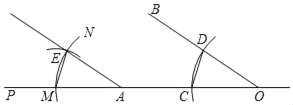
①以点O为圆心，OC为半径画弧，交OB于点D，连接CD
②以点A为圆心，OC为半径画弧MN，交AP于点M
③以点M为圆心，CD为半径画弧，交MN于点E，连接ME，作射线AE
如图所示，则下列结论不成立的是( )
A. CD∥EM B. AE∥OB C. ∠ODC＝∠AEM D. ∠OAE＝∠BDC
-
科目： 来源： 题型：
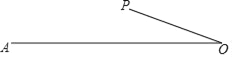
查看答案和解析>>【题目】如图，线段OA＝2，OP＝1，将线段OP绕点O任意旋转时，线段AP的长度也随之改变，则下列结论：
①AP的最小值是1，最大值是4；
②当AP＝2时，△APO是等腰三角形；
③当AP＝1时，△APO是等腰三角形；
④当AP＝
时，△APO是直角三角形；⑤当AP＝
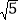时，△APO是直角三角形．其中正确的是( )
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
-
科目： 来源： 题型：
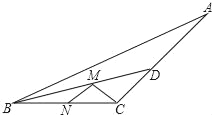
查看答案和解析>>【题目】如图，钝角三角形△ABC的面积是15，最长边AB＝10，BD平分∠ABC，点M，N分别是BD，BC上的动点，则CM+MN的最小值为_____
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，△ABC中，∠ACB＝90°，AC＝3
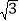，BC＝3，如图②，将△ABC沿一条直线折叠，使得点A与点C重合(1)在图①中画出折痕所在的直线l，设直线l与AB，AC分别相交于点D，E(尺规作图，不写作法，保留作图痕迹)
(2)如图②，求△CDB的周长．
-
科目： 来源： 题型：
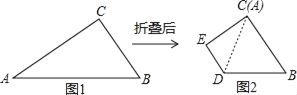
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，3）．
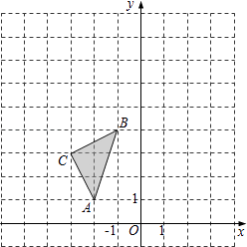
（1）画出△ABC关于y轴对称的△A1B1C1 ， 并写出A1点的坐标及sin∠B1A1C1的值；
以原点O为位似中心，位似比为1：2，在y轴的左侧，画出 将△ABC放大后的△A2B2C2 ， 并写出A2点的坐标；
（2）若点D（a，b）在线段AB上，直接写出经过（2）的变化后点D的对应点D2的坐标． -
科目： 来源： 题型：
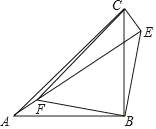
查看答案和解析>>【题目】如图，点E是等腰三角形纸片ABC外一点，∠ABC＝90°，连接AE，点F是线段AE(不与点A，E重合)上一点，在△EBF中，EB＝FB，∠EBF＝90°，连接CE，CF
(1)求证：△ABF≌△CBE；
(2)判断△CEF的形状，并说明理由．
相关试题
