【题目】如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE. 
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径.
参考答案:
【答案】
(1)证明:∵AD平分∠BAC,
∴∠CAD=∠EAD,
∴ ![]() =
= ![]() ,
,
∴CD=ED
∵∠ACD=90°,
∴AD是⊙O的直径,
∴ ![]() =
= ![]() ,
,
∴AC=AE
(2)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB= ![]() =10,
=10,
BE=10﹣AE=10﹣6=4,
设CD=DE=x,
BD=8﹣x,
在Rt△BDE中.BD2=DE2+BE2
(8﹣x)2+x2=42
x=3,即BD=3,
在Rt△ACD中,AD= ![]() =3
=3 ![]()
【解析】(1)根据角平分线的性质、圆周角、弧、弦之间的关系得到 ![]() =
= ![]() ,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
【考点精析】认真审题,首先需要了解三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将△ABC顶点的横坐标增加4个单位,纵坐标不变,三角形将如何变化?若将△ABC顶点横坐标都乘以-1,纵坐标不变,三角形将如何变化?

-
科目: 来源: 题型:
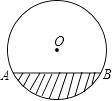
查看答案和解析>>【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少?
-
科目: 来源: 题型:
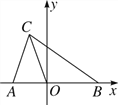
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且
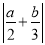 +(4a-b+11)2=0.
+(4a-b+11)2=0.(1)求a,b的值;
(2)在y轴的负半轴上存在一点M,使△COM的面积等于△ABC面积的一半,求出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C,D分别表示-3,-1
 ,0,4.请解答下列问题:
,0,4.请解答下列问题:(1)在数轴上描出A,B,C,D四个点;
(2)现在把数轴的原点取在点B处,其余均不变,那么点A,B,C,D分别表示什么数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,上七年级的小贝在一张纸上画了一条数轴,妹妹不知道它有什么用处,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
(1)被小猫遮住的是正数还是负数?
(2)被小狗遮住的整数有几个?
(3)此时小猫和小狗之间(即点A,B之间)的整数有几个?

相关试题

