【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少? 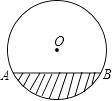
参考答案:
【答案】解:过点O做OC⊥AB于点D,连接OA.
设半径长为rcm,
∵OC⊥AB,
∴AD= ![]() AB
AB
= ![]() ×8
×8
=4(cm),
∵CD=2cm∴OD=r﹣2(cm)
在Rt△AOD中,由勾股定理得:(r﹣2)2+42=r2
r2﹣4r+4+42=42
4r=20
r=5,
答:该水管的半径是5cm.
【解析】先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD= ![]() AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
【考点精析】通过灵活运用垂径定理的推论,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
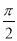 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )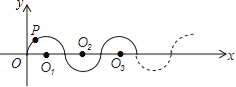
A. (2014,0) B. (2015,﹣1) C. (2015,1) D. (2016,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)x2+6x﹣1=0
(2)(2x+3)2﹣25=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将△ABC顶点的横坐标增加4个单位,纵坐标不变,三角形将如何变化?若将△ABC顶点横坐标都乘以-1,纵坐标不变,三角形将如何变化?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且
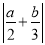 +(4a-b+11)2=0.
+(4a-b+11)2=0.(1)求a,b的值;
(2)在y轴的负半轴上存在一点M,使△COM的面积等于△ABC面积的一半,求出点M的坐标.
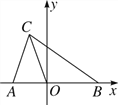
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.

(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

相关试题

