【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )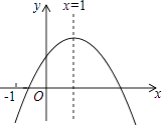
A.1
B.2
C.3
D.4
参考答案:
【答案】D
【解析】解:开口向下,a<0,抛物线与y轴交于正半轴,c>0,根据对称轴为x=﹣ ![]() >0,则b>0,所以abc<0,①正确;
>0,则b>0,所以abc<0,①正确;
根据x=﹣1时y<0,所以a﹣b+c<0,②正确;
根据对称轴为x=1,即﹣ ![]() =1,2a+b=0,③正确;
=1,2a+b=0,③正确;
由抛物线与x轴有两个交点,所以b2﹣4ac>0,④正确
所以答案是:D
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数中,y的值随着x值的增大而减小的是( )
A.y=2x
B.y=x+1
C.y= (x>0)
(x>0)
D.y=x2(x>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A、B两种商品很快售完,该商场决定再一次购进A、B两种商品共35件,如果将这35件商品全部售完后所得利润高于4000元,那么该商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.

(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.
(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.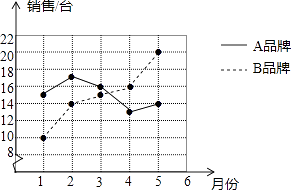
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.

(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形AOCF是菱形.
相关试题

