【题目】△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.

(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
参考答案:
【答案】(1)∠DAE=11°;(2)∠DAE=![]() (∠C﹣∠B);说明见解析;(3)∠G=45°.
(∠C﹣∠B);说明见解析;(3)∠G=45°.
【解析】
(1)根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠DAE=∠DAC-∠EAC,即可得出;
(2)根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠DAE=∠DAC-∠EAC,即可得出;
(3)设∠ACB=α,根据角平分线的定义得到∠CAG=![]() ∠EAC=
∠EAC=![]() (90°-α)=45°-
(90°-α)=45°-![]() α,∠BCG=
α,∠BCG=![]() ∠BCF=
∠BCF=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,根据三角形的内角和即可得到结论.
α,根据三角形的内角和即可得到结论.
解:(1)∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,
∵AD是∠BAC的平分线,
∴∠DAC=![]() ∠BAC=39°,
∠BAC=39°,
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C=90°﹣62°=28°,
∴∠DAE=∠DAC﹣∠EAC=39°﹣28°=11°;
(2)∵∠BAC=180°﹣∠B﹣∠C,
∵AD是∠BAC的平分线,
∴∠DAC=![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣![]() (∠B+∠C)﹣(90°﹣∠C)=
(∠B+∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B);
(∠C﹣∠B);
(3)设∠ACB=α,
∵AE⊥BC,
∴∠EAC=90°﹣α,∠BCF=180°﹣α,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=![]() ∠EAC=
∠EAC=![]() (90°﹣α)=45°﹣
(90°﹣α)=45°﹣![]() α,
α,
∠BCG=![]() ∠BCF=
∠BCF=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠G=180°﹣∠GAC﹣∠ACG=180°﹣(45°﹣![]() α)﹣α﹣(90°﹣
α)﹣α﹣(90°﹣![]() α)=45°.
α)=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.
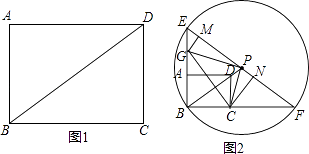
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数中,y的值随着x值的增大而减小的是( )
A.y=2x
B.y=x+1
C.y= (x>0)
(x>0)
D.y=x2(x>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A、B两种商品很快售完,该商场决定再一次购进A、B两种商品共35件,如果将这35件商品全部售完后所得利润高于4000元,那么该商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )
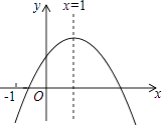
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.
(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.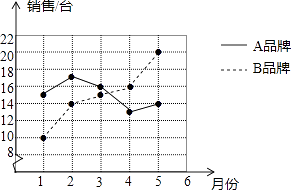
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

相关试题

