【题目】如图,点O是坐标原点,矩形OABC的顶点A,C分别在坐标轴上,点B的坐标为(4,2).直线![]() 分别交AB,BC于点M,N,反比例函数
分别交AB,BC于点M,N,反比例函数![]() 的图像经过点M.
的图像经过点M.
(1)求反比例函数的解析式;
(2)判断点N是否在反比例函数![]() 的图像上?试说明理由.
的图像上?试说明理由.

参考答案:
【答案】(1)反比例函数的解析式是![]() ; (2)点N在反比例函数
; (2)点N在反比例函数 ![]() 上.
上.
【解析】试题分析:(1)求出OA=BC=2,将y=2代入y=﹣![]() x+3求出x=2,得出M的坐标,把M的坐标代入反比例函数的解析式即可求出答案;
x+3求出x=2,得出M的坐标,把M的坐标代入反比例函数的解析式即可求出答案;
(2)把x=4代入直线解析式,求出N的坐标,再判断点N是否在反比例函数的图象上.
试题解析:解:(1)∵B(4,2),四边形OABC是矩形,∴OA=BC=2,将y=2代入y=﹣![]() x+3得:x=2,∴M(2,2),把M的坐标代入
x+3得:x=2,∴M(2,2),把M的坐标代入![]() 得:k=4,∴反比例函数的解析式是
得:k=4,∴反比例函数的解析式是![]() ;
;
(2)把x=4代入y=﹣![]() x+3:得:y=1,∴N(4,1),把x=4代入
x+3:得:y=1,∴N(4,1),把x=4代入![]() ,得:y=1,∴点N在反比例函数
,得:y=1,∴点N在反比例函数![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
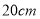 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:三角形的直角边长/

1
2
3
4
5
6
7
8
9
10
阴影部分的面积/
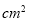
398
392
382
368
350
302
272
200

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由
 增加到
增加到 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?(4)设等腰直角三角形的直角边长为
 ,图中阴影部分的面积为
,图中阴影部分的面积为 ,写出
,写出 与
与 的关系式.
的关系式. -
科目: 来源: 题型:
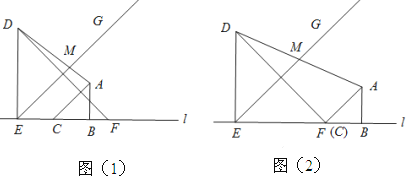
查看答案和解析>>【题目】如图1,两个等腰直角三角板
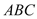 和
和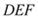 有一条边在同一条直线
有一条边在同一条直线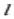 上,
上,  ,
,  .将射线
.将射线 绕点
绕点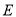 逆时针旋转
逆时针旋转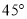 ,交直线
,交直线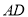 于点
于点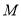 .将图1中的三角板
.将图1中的三角板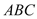 沿直线
沿直线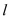 向右平移,设
向右平移,设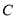 、
、 两点间的距离为
两点间的距离为 .
.
解答问题:
(1)①当点
 与点
与点 重合时,如图2所示,可得
重合时,如图2所示,可得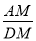 的值为 ;
的值为 ; ②在平移过程中,
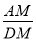 的值为 (用含
的值为 (用含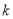 的代数式表示);
的代数式表示); (2)将图2中的三角板
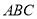 绕点
绕点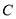 逆时针旋转,原题中的其他条件保持不变.当点
逆时针旋转,原题中的其他条件保持不变.当点 落在线段
落在线段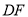 上时,如图3所示,计算
上时,如图3所示,计算 的值;
的值; 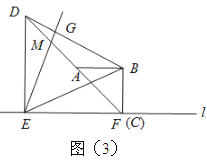
(3)将图1中的三角板ABC绕点C逆时针旋转
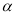 度,
度, 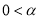 ≤
≤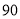 ,原题中的其他条件保持不变.如图4所示,请补全图形,计算
,原题中的其他条件保持不变.如图4所示,请补全图形,计算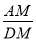 的值(用含k的代数式表示).
的值(用含k的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
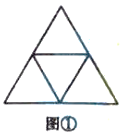
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有
 个;
个;边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有
 个;边长为2的正三角形共有
个;边长为2的正三角形共有 个.
个.
探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
-
科目: 来源: 题型:
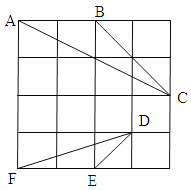
查看答案和解析>>【题目】如图,在4×4的正方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC , BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 经过点
经过点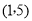 和
和 ,分别与x轴、y轴交于A、B两点.
,分别与x轴、y轴交于A、B两点.(1)求直线
 的解析式:
的解析式:(2)若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有 个;
(3)作出点
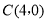 关于直线
关于直线 的对称点
的对称点 ,则点
,则点 的坐标为 ;
的坐标为 ;
(4)若在直线
 和
和 轴上分别存在一点
轴上分别存在一点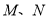 使
使 的周长最短,请在图中标出点
的周长最短,请在图中标出点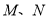 (不写作法,保留痕迹).
(不写作法,保留痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3个红球和2个黑球,两人先后从袋中取出一个球(不放回),若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1)请用树状图法求出摸笔游戏所有可能的结果;
(2)计算小明获胜的概率是 ,小军获胜的概率是 ,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
相关试题

