【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
参考答案:
【答案】(1) 自变量:三角形的直角边长,因变量:阴影部分的面积;(2)见解析;(3) ![]() .
.
【解析】
(1)根据定义确定自变量、因变量即可;
(2)根据题意计算即可;
(3)观察数据表格确定阴影面积变化趋势;
(4)阴影面积为正方形面积减去四个等腰直角三角形面积.
解:(1)在这个变化过程中,自变量:三角形的直角边长,因变量:阴影部分的面积;
(2)等腰直角三角形直角边长为6时,阴影面积为202-4×![]() ×62=328,
×62=328,
等腰直角三角形直角边长为9时,阴影面积为202-4×![]() ×92=238;
×92=238;
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 328 | 238 |
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积由
时,阴影部分的面积由![]() 减小到
减小到![]() ;
;
(4)![]() .
.
故答案为:(1) 自变量:三角形的直角边长,因变量:阴影部分的面积; (2)见解析; (3) ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】淮河汛期即将来临,防汛指挥部在一危险地带两岸各安置了-探照灯,便于夜间查看河面及两岸河堤的情况.如图,灯
 射线自
射线自 顺时针旋转至
顺时针旋转至 便立即回转,灯
便立即回转,灯 射线自
射线自 顺时针旋转至
顺时针旋转至 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯 转动的速度是
转动的速度是 /秒,灯
/秒,灯 转动的速度是
转动的速度是 /秒,且
/秒,且 满足:
满足: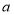 是
是 的整数部分,
的整数部分, 是不等式
是不等式 的最小整数解.假定这- -带淮河两岸河堤是平行的,即
的最小整数解.假定这- -带淮河两岸河堤是平行的,即 ,且
,且 .
.
(1)如图1,
 _____,
_____, ;
;(2)若灯
 射线先转动
射线先转动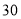 秒,灯
秒,灯 射线才开始转动,在灯
射线才开始转动,在灯 射线到达
射线到达 之前,
之前, 灯转动几秒,两灯的光東互相平行?
灯转动几秒,两灯的光東互相平行?(3)如图2,两灯同时转动,在灯A射线到达AN之前。若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1955年,印度数学家卡普耶卡(
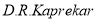 )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数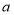 ,用
,用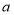 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数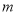 ,再减去它的反序数
,再减去它的反序数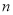 (即将
(即将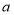 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数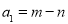 ,然后继续对
,然后继续对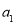 重复上述变换,得数
重复上述变换,得数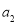 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论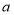 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行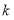 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数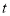 ,这个数称为
,这个数称为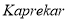 变换的核.则四位数9631的
变换的核.则四位数9631的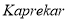 变换的核为______.
变换的核为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,两个等腰直角三角板
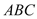 和
和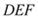 有一条边在同一条直线
有一条边在同一条直线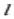 上,
上,  ,
,  .将射线
.将射线 绕点
绕点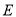 逆时针旋转
逆时针旋转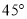 ,交直线
,交直线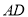 于点
于点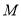 .将图1中的三角板
.将图1中的三角板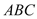 沿直线
沿直线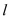 向右平移,设
向右平移,设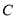 、
、 两点间的距离为
两点间的距离为 .
.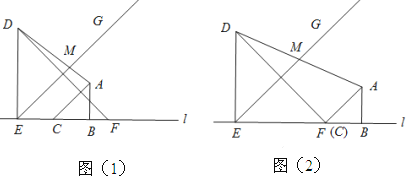
解答问题:
(1)①当点
 与点
与点 重合时,如图2所示,可得
重合时,如图2所示,可得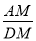 的值为 ;
的值为 ; ②在平移过程中,
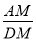 的值为 (用含
的值为 (用含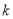 的代数式表示);
的代数式表示); (2)将图2中的三角板
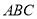 绕点
绕点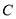 逆时针旋转,原题中的其他条件保持不变.当点
逆时针旋转,原题中的其他条件保持不变.当点 落在线段
落在线段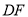 上时,如图3所示,计算
上时,如图3所示,计算 的值;
的值; 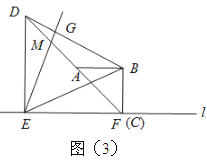
(3)将图1中的三角板ABC绕点C逆时针旋转
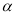 度,
度, 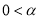 ≤
≤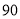 ,原题中的其他条件保持不变.如图4所示,请补全图形,计算
,原题中的其他条件保持不变.如图4所示,请补全图形,计算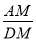 的值(用含k的代数式表示).
的值(用含k的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
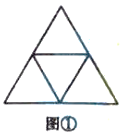
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有
 个;
个;边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有
 个;边长为2的正三角形共有
个;边长为2的正三角形共有 个.
个.
探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是坐标原点,矩形OABC的顶点A,C分别在坐标轴上,点B的坐标为(4,2).直线
 分别交AB,BC于点M,N,反比例函数
分别交AB,BC于点M,N,反比例函数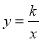 的图像经过点M.
的图像经过点M.(1)求反比例函数的解析式;
(2)判断点N是否在反比例函数
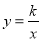 的图像上?试说明理由.
的图像上?试说明理由. 
相关试题

