【题目】如图,已知直线![]() 经过点
经过点![]() 和
和![]() ,分别与x轴、y轴交于A、B两点.
,分别与x轴、y轴交于A、B两点.
(1)求直线![]() 的解析式:
的解析式:
(2)若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有 个;
(3)作出点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;![]()
(4)若在直线![]() 和
和![]() 轴上分别存在一点
轴上分别存在一点![]() 使
使![]() 的周长最短,请在图中标出点
的周长最短,请在图中标出点![]() (不写作法,保留痕迹).
(不写作法,保留痕迹).

参考答案:
【答案】(1)![]() ;(2)10;(3)作图见解析,D(6,2);(4)作图见解析
;(2)10;(3)作图见解析,D(6,2);(4)作图见解析
【解析】
(1)先利用待定系数法求得直线AB的解析式为![]() ;
;
(2)分别把x=2、3、4、5代入,求出对应的纵坐标,从而得到图中阴影部分(不包括边界)所含格点的坐标;
(3)首先作出点C关于直线AB的对称点D,根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D的坐标;
(4)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.
(1)设直线AB的解析式为![]() ,
,
把(1,5),(4,2)代入得,![]() ,
,
解得![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)当x=2,y=4;
当x=3,y=3;
当x=4,y=2;
当x=5,y=1.
∴图中阴影部分(不包括边界)所含格点的有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),
(3,1),(3,2),
(4,1).
一共10个;
故答案为:10;
(3)如图,点D就是所求作的点;
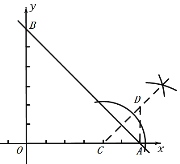
∵直线![]() 与
与![]() 轴、y轴交于A、B两点,
轴、y轴交于A、B两点,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴A点坐标为(6,0),B点坐标为(0,6),
∴OA=OB=6,∠OAB=45°.
∵点C关于直线AB的对称点为D,点C(4,0),
∴AD=AC=2,AB⊥CD,
∴∠DAB=∠CAB=45°,
∴∠DAC=90°,
∴点D的坐标为(6,2);
(4)如图,点M、N就是所求的点;
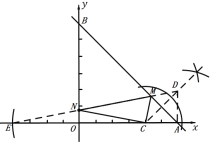
作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则NC=NE,点E(-4,0).
又∵点C关于直线AB的对称点为D,
∴CM=DM,
∴△CMN的周长=CM+MN+NC=DM+MN+NE=DE,此时周长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
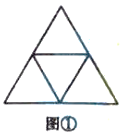
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有
 个;
个;边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有
 个;边长为2的正三角形共有
个;边长为2的正三角形共有 个.
个.
探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为
 的正三角形的三条边分别
的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是坐标原点,矩形OABC的顶点A,C分别在坐标轴上,点B的坐标为(4,2).直线
 分别交AB,BC于点M,N,反比例函数
分别交AB,BC于点M,N,反比例函数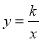 的图像经过点M.
的图像经过点M.(1)求反比例函数的解析式;
(2)判断点N是否在反比例函数
 的图像上?试说明理由.
的图像上?试说明理由. 
-
科目: 来源: 题型:
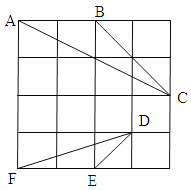
查看答案和解析>>【题目】如图,在4×4的正方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC , BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3个红球和2个黑球,两人先后从袋中取出一个球(不放回),若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1)请用树状图法求出摸笔游戏所有可能的结果;
(2)计算小明获胜的概率是 ,小军获胜的概率是 ,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的中点,
的中点, ,
, .动点
.动点 从点
从点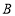 出发,沿
出发,沿 方向以
方向以 的速度向点
的速度向点 运动;同时动点
运动;同时动点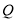 从点
从点 出发,沿
出发,沿 方向以
方向以 的速度向点
的速度向点 运动,运动时间是
运动,运动时间是 秒.
秒.
(1)用含
 的代数式表示
的代数式表示 的长度.
的长度.(2)在运动过程中,是否存在某一时刻
 ,使点
,使点 位于线段
位于线段 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)是否存在某一时刻
 ,使
,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(4)是否存在某一时刻
 ,使
,使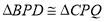 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

