Question

【题目】如图，抛物线与轴交于，两点（点在轴的正半轴上），与轴交于点，矩形的一条边在线段上，顶点，分别在线段，上．

求点，，的坐标；

若点的坐标为，矩形的面积为，求关于的函数表达式，并指出的取值范围；

当矩形的面积取最大值时，

①求直线的解析式；

②在射线上取一点，使，若点恰好落在该抛物线上，则________．

Answer 1

【答案】⑴：,,；⑵；⑶：①；②.

【解析】

(1)令x＝0求出抛物线与x轴的交点坐标，令x＝0求出抛物线与y轴交点坐标；

(2)先表示出BE，DE，用矩形的面积公式求解即可；(3)①由(2)得到的矩形面积的函数关系式，面积最大时求出m，从而确定出D，F坐标，即可得出直线解析式；②先确定出直线DF和抛物线的交点坐标，用比例式求出k.

(1)∵抛物线与x轴交于A，B两点(点A在x轴的正半轴上)，∴令y＝0，即，∴x＝－4或x＝2，令，∴，∴,,；

(2)由(1)知，OA＝2，OC＝4，AD＝2－m，∵DG∥OC，∴，∴DG＝4－2m，同理BE＝4－2m，∴DE＝AB－AD－BE＝3m，∴；

(3)①由(2)得，；当m＝1时，矩形DEFG面积最大，最大面积为6，此时，，，，，∴直线DF的解析式为；

②如图

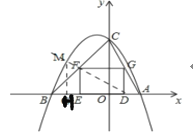
由①知，D(1,0)，F(－2,2)，∴，∴FM＝k×DF＝，过点M作MH⊥x轴，设则∴，∵点M在抛物线上，∴，∴，∵，∴，∴，∵，，∴，∵,∴,∴，∴，故答案为.