【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】B
【解析】
阅读题目,先利用待定系数法求得该函数解析式,根据a的值即可判断(1) ;接下来根据函数解析式可得函数对称轴,根据二次函数的性质判断(2)(3) ;对于(4),由y=ax2+bx+c (a,b,c为常数,且a≠0)的图象与x轴有两个交点,顶点坐标的纵坐标>5,可得方程ax2+bx+c=5根的情况,据此判断即可,至此问题得解.
由图表中数据可得出:x=-1时,y=-1,x=0时,y=3,x=1时,y=5,则有 ,解得
,解得 ,则y=-x2+3x+3=-(x-
,则y=-x2+3x+3=-(x-![]() )2+
)2+![]() ,因为a=-1<0,所以(1)正确,因为该函数的对称轴x=
,因为a=-1<0,所以(1)正确,因为该函数的对称轴x=![]() ,所以当x<0时,y<3,故(2)正确,根据二次函数的性质可得到x>
,所以当x<0时,y<3,故(2)正确,根据二次函数的性质可得到x>![]() 时,y的值随x值的增大而减小,x<
时,y的值随x值的增大而减小,x<![]() 时,y的值随x的值的增大而增大,故(3)错误,因为y=ax2+bx+c的图象与x轴有交点,顶点坐标的纵坐标>5,所以方程ax2+bx+c=5,有两个不相等的实数根,故(4)正确,故答案选B.
时,y的值随x的值的增大而增大,故(3)错误,因为y=ax2+bx+c的图象与x轴有交点,顶点坐标的纵坐标>5,所以方程ax2+bx+c=5,有两个不相等的实数根,故(4)正确,故答案选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字﹣乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (
( ,
, 、
、 、
、 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列 个结论:①
个结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ 为常数,且
为常数,且 .其中正确的结论有( )
.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点 ,顶点为点
,顶点为点 ,点
,点 与点
与点 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
 求直线
求直线 的解析式;
的解析式; 点
点 在抛物线上,且点
在抛物线上,且点 的横坐标为
的横坐标为 .将抛物线在点
.将抛物线在点 ,
, 之间的部分(包含点
之间的部分(包含点 ,
, )记为图象
)记为图象 ,若图象
,若图象 向下平移
向下平移 个单位后与直线
个单位后与直线 只有一个公共点,求
只有一个公共点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1 、y2 (km), y1 、y2 与x的函数关系如图所示.

(1)填空:A、C两港口间的距离为_______km,
 _______;
_______;(2)求图中点P的坐标;
(3)若两船的距离不超过8km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在
在 轴的正半轴上),与
轴的正半轴上),与 轴交于点
轴交于点 ,矩形
,矩形 的一条边
的一条边 在线段
在线段 上,顶点
上,顶点 ,
,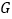 分别在线段
分别在线段 ,
, 上.
上.
 求点
求点 ,
, ,
, 的坐标;
的坐标; 若点
若点 的坐标为
的坐标为 ,矩形
,矩形 的面积为
的面积为 ,求
,求 关于
关于 的函数表达式,并指出
的函数表达式,并指出 的取值范围;
的取值范围; 当矩形
当矩形 的面积
的面积 取最大值时,
取最大值时,①求直线
 的解析式;
的解析式;②在射线
 上取一点
上取一点 ,使
,使 ,若点
,若点 恰好落在该抛物线上,则
恰好落在该抛物线上,则 ________.
________.
相关试题

