【题目】【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“妙分线”.
【解决问题】
(1)如图2,若∠MPN= ![]() ,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含
,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含![]() 的代数式表示出所有可能的结果)
的代数式表示出所有可能的结果)
【深入研究】
如图2,若∠MPN=54°,且射线PQ绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当PQ与PN成![]() 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.
(2)当t为何值时,射线PM是∠QPN的“妙分线”.
(3)若射线PM同时绕点P以每秒6°的速度顺时针旋转,并与PQ同时停止.请求出当射线PQ 是∠MPN的“妙分线”时t的值.

参考答案:
【答案】(![]() )
)![]() ,
, ![]() ,
, ![]() ;(
;(![]() )
)![]() ,
, ![]() ,
, ![]() ;(
;(![]() )
)![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)分3种情况,根据妙分线定义即可求解;
(2)分3种情况,根据妙分线定义即可求解;
(3)分3种情况,根据妙分线定义即可求解.
试题解析:解:(1)∵∠MPN=α,∴∠MPQ=![]() α或
α或![]() α或
α或![]() α;
α;
故答案为: ![]() α或
α或![]() α或
α或![]() α;
α;
(2)依题意有
①8t=54+![]() ×54,解得t=
×54,解得t=![]() ;
;
②8t=2×54,解得t=![]() ;
;
③8t=54+2×54,解得t=![]() .
.
故当t为![]() s或
s或![]() s或
s或![]() s时,射线PM是∠QPN的“妙分线”;
s时,射线PM是∠QPN的“妙分线”;
(3)依题意有
①8t=![]() (6t+54),解得t=3;
(6t+54),解得t=3;
②8t=![]() (6t+54),解得t=5.4;
(6t+54),解得t=5.4;
③8t=![]() (6t+54),解得t=9.
(6t+54),解得t=9.
故当t为3s或5.4s或9s时,射线PQ是∠MPN的“妙分线”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
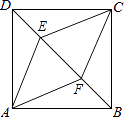
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算结果为a5的是( )
A.(a2)3B.a2+a3C.a2a3D.a10÷a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在教室里确定某同学的座位需要的数据个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)如图,平面上有四个点A,B,C,D.

(1)根据下列语句画图:
①画射线BA;
②画直线AD,BC相交于点E;
③延长线段DC,在线段DC的延长线上取一点F,使CF=BC;
④连接EF.
(2)图中以E为顶点的角中,小于平角的角共有 个.
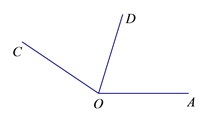
(Ⅱ)已知:∠AOC=146°,OD为∠AOC的平分线,∠AOB=90°,部分图形如图所示.请补全图形,并求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
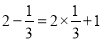 ,
, 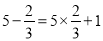 ,给出定义如下:
,给出定义如下:我们称使等式
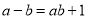 成立的一对有理数
成立的一对有理数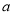 ,
, 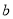 为“共生有理数对”,记为(
为“共生有理数对”,记为( ,
, 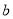 ),如:数对(
),如:数对(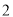 ,
, 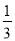 ),(
),(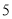 ,
, 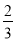 ),都是“共生有理数对”.
),都是“共生有理数对”.(1)判断数对(
 ,
, 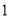 ),(
),(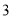 ,
, 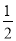 )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;(2)若(
 ,
, 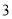 )是“共生有理数对”,求
)是“共生有理数对”,求 的值;
的值;(3)若(
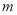 ,
, 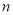 )是“共生有理数对”,则(
)是“共生有理数对”,则( ,
, 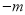 ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:20202﹣20192=_____.
相关试题

