【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 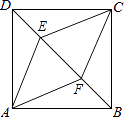
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
参考答案:
【答案】
(1)解:四边形AECF是菱形,理由如下:
连接AC,交BD于点O,

∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形
(2)解:∵EF=4,DE=BF=2,
∴AC=BD=8,
∴AE= ![]() ,
,
∴四边形AECF的周长为8 ![]()
【解析】(1)连接AC,交BD于点O.利用正方形的性质得出AC⊥BD,OA=OC=OB=OD,进一步得出OE=OF,证得四边形AECF是菱形;(2)利用菱形的性质和勾股定理求得即可.
【考点精析】利用勾股定理的概念和菱形的判定方法对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3x2y-5xy)·(-4xy2)=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l:y=kx+5k+12(k≠0),当k变化时,原点到这条直线的距离的最大值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
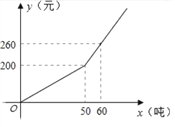
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收
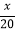 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算结果为a5的是( )
A.(a2)3B.a2+a3C.a2a3D.a10÷a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在教室里确定某同学的座位需要的数据个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“妙分线”.
【解决问题】
(1)如图2,若∠MPN=
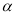 ,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含
,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含 的代数式表示出所有可能的结果)
的代数式表示出所有可能的结果)【深入研究】
如图2,若∠MPN=54°,且射线PQ绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当PQ与PN成
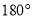 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.(2)当t为何值时,射线PM是∠QPN的“妙分线”.
(3)若射线PM同时绕点P以每秒6°的速度顺时针旋转,并与PQ同时停止.请求出当射线PQ 是∠MPN的“妙分线”时t的值.

相关试题

