搜索
【题目】计算：20202﹣20192＝_____．
参考答案：
【答案】4039
【解析】
根据平方差公式：a2﹣b2＝（a+b）（a﹣b）计算即可．
解：原式＝（2020+2019）×（2020﹣2019）＝4039，
故答案为：4039
-
科目： 来源： 题型：
查看答案和解析>>【题目】【探索新知】
如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB、∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“妙分线”．
【解决问题】
（1）如图2，若∠MPN=
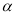，且射线PQ是∠MPN的“妙分线”，则∠NPQ= ____ ．（用含
的代数式表示出所有可能的结果）【深入研究】
如图2，若∠MPN=54°，且射线PQ绕点P从PN位置开始，以每秒8°的速度顺时针旋转，当PQ与PN成
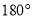时停止旋转，旋转的时间为t秒．（2）当t为何值时，射线PM是∠QPN的“妙分线”．
（3）若射线PM同时绕点P以每秒6°的速度顺时针旋转，并与PQ同时停止．请求出当射线PQ 是∠MPN的“妙分线”时t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（Ⅰ）如图，平面上有四个点A，B，C，D．
（1）根据下列语句画图:
①画射线BA；
②画直线AD，BC相交于点E；
③延长线段DC，在线段DC的延长线上取一点F，使CF=BC；
④连接EF．
（2）图中以E为顶点的角中，小于平角的角共有 个．
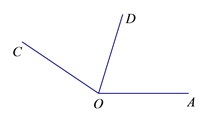
（Ⅱ）已知：∠AOC=146°，OD为∠AOC的平分线，∠AOB=90°，部分图形如图所示．请补全图形，并求∠BOD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列两个等式：
， 
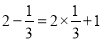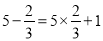，给出定义如下：我们称使等式
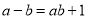成立的一对有理数
， 
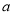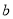为“共生有理数对”，记为（
， 
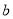），如：数对（
， 
），（
， 
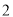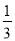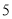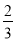），都是“共生有理数对”．（1）判断数对（
， 
），（
， 
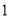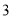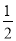）是不是“共生有理数对”，写出过程；（2）若（
， 
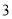）是“共生有理数对”，求
的值；（3）若（
， 
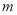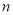）是“共生有理数对”，则（
， 
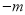） “共生有理数对”（填“是”或“不是”）；说明理由；（4）请再写出一对符合条件的 “共生有理数对”为 （注意：不能与题目中已有的“共生有理数对”重复）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某股票市场，买、卖股票都要分别交纳印花税等有关税费．以A市股的股票交易为例，除成本外还要交纳：
①印花税：按成交金额的0.1%计算；
②过户费：按成交金额的0.1%计算；
③佣金：按不高于成交金额的0.3%计算（本题按0.3%计算），不足5元按5元计算，
例：某投资者以每股5.00元的价格在沪市A股中买入股票“金杯汽车”1000股，以每股5.50元的价格全部卖出，共盈利多少？
解：直接成本：5×1000=5000（元）；
印花税：（5000+5.50×1000）×0.1%=10.50（元）；
过户费：（5000+5.50×1000）×0.1%=10.50（元）；
佣金：5000×0.3%=15.00（元） 5.50×1000×0.3%=16.50（元）
∵15.00>5 16.50>5 ∴佣金为15.00+16.50=31.50元．
总支出：5000+10.50+10.50+31.50=5052.50（元）；
总收入：5.50×1000=5500（元）；
总盈利：5500-5052.50=447.50（元）．
问题：
（1）小王对此很感兴趣，以每股5.00元的价格买入以上股票100股，以每股5.50元的价格全部卖出，则他盈利为______________元；
（2）小张以每股a（a≥5）元的价格买入以上股票1000股，股市波动大，他准备在不亏不盈时卖出．请你帮他计算出卖出的价格每股是多少元（用a的代数式表示）？
（3）小张再以每股5.00元的价格买入以上股票1000股，准备盈利1000元时才卖出，请你帮他计算卖出的价格每股是多少元？（精确到0.01元）
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简再求值，（3a﹣2）2﹣3a（2a﹣1）+5，其中a是方程x2﹣3x+1＝0的解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．
【类比引申】如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时，仍有EF=BE+FD．
【探究应用】如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（
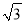﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据： 
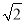=1.41， 
=1.73）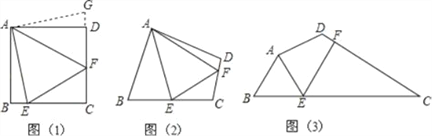
相关试题
