【题目】已知二次函数y=![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=![]() 与x轴交于A(
与x轴交于A(![]() ,0)、B(
,0)、B(![]() ,0)两点,且
,0)两点,且![]() <
<![]() ,
,![]() =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,试探究
)两点,试探究![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
参考答案:
【答案】(1) k<![]() ,且k≠0;(2) k<0;x<
,且k≠0;(2) k<0;x<![]() ;(3)1,理由详见解析.
;(3)1,理由详见解析.
【解析】
试题分析:(1)根据题意k≠0,△>0,列出不等式组即可解决问题.
(2)设反比例函数解析式为y=![]() ,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.
,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.
(3)结论:![]() =1.令y=0,则有
=1.令y=0,则有![]() =0,所以
=0,所以![]() +
+![]() =
=![]() ,
,![]() =
=![]() ,根据
,根据![]() =34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,由
=34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,由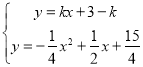 消去y得
消去y得![]() +(4k﹣2)x﹣3﹣4k=0,得
+(4k﹣2)x﹣3﹣4k=0,得![]() =﹣(4k﹣2),
=﹣(4k﹣2),![]() =﹣3﹣4k,根据
=﹣3﹣4k,根据![]() =
=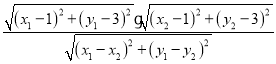 ,代入化简即可解决问题.
,代入化简即可解决问题.
试题解析:(1)∵二次函数y=![]() 与x轴有两个不同的交点,
与x轴有两个不同的交点,
∴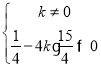 ,
,
解得k<![]() ,且k≠0.
,且k≠0.
所以若该函数的图象与x轴有两个不同的交点,k的取值范围是k<![]() ,且k≠0;
,且k≠0;
(2)设反比例函数解析式为y=![]() ,
,
∵经过点(1,k),
∴m=k,
∵反比例函数和二次函数y=![]() 都是y随x的增大而增大,
都是y随x的增大而增大,
∴k<0,x<![]() ,即x<
,即x<![]() .
.
(3)结论:![]() =1.
=1.
理由:令y=0,则有![]() =0,
=0,
∴![]() +
+![]() =
=![]() ,
,![]() =
=![]()
∵![]() =34,
=34,
∴![]() =34,
=34,
∴![]() =0,
=0,
解得k=![]() 或
或![]() ,
,
由(1)可知k<![]() ,
,
∴k=![]() ,
,
∴抛物线解析式为y=![]() ,
,
设过点P的直线为y=kx+b,把P(1,3)代入得3=k+b,
∴b=3﹣k,
∴过点P的直线为y=kx+3﹣k,
∵过点P的直线为y=kx+3﹣k与物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,
)两点,
∴![]() =k
=k![]() +3﹣k,
+3﹣k,![]() =k
=k![]() +3﹣k,
+3﹣k,
由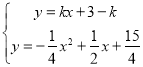 消去y得
消去y得![]() +(4k﹣2)x﹣3﹣4k=0,
+(4k﹣2)x﹣3﹣4k=0,
∴![]() =﹣(4k﹣2),
=﹣(4k﹣2),![]() =﹣3﹣4k ,
=﹣3﹣4k ,
∴![]() =
=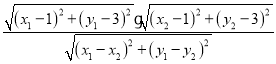 =
=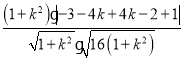 =1.
=1.
-
科目: 来源: 题型:
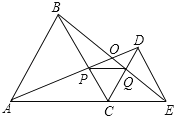
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决有关问题:我们知道|x|=
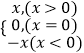 ,
,
所以当x>0时,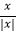 =
= 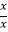 =1; 当x<0时,
=1; 当x<0时, 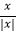 =
= 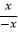 =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时,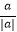 +
+ 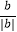 =;
=;
(2)已知a,b是有理数,当abc≠0时,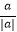 +
+ 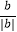 +
+ 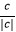 =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 +
+  +
+ 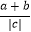 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠1与∠2互为余角,∠1与∠3互为补角,那么下列结论: ①∠3﹣∠2=90° ②∠3+∠2=270°﹣2∠1 ③∠3﹣∠1=2∠2 ④∠3>∠1+∠2.
正确的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间7名工人日加工零件数分别为4,5,10,5,5,4,10则这组数据的众数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续走了1.5千米到达小红家,又向西走了10千米到达小刚家,最后回到百货大楼.
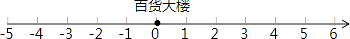
(1)以百货大楼为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.05升,那么这辆货车共耗油多少升?
相关试题

