【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续走了1.5千米到达小红家,又向西走了10千米到达小刚家,最后回到百货大楼. ![]()
(1)以百货大楼为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.05升,那么这辆货车共耗油多少升?
参考答案:
【答案】
(1)解:如图所示:A、B、C分别表示小明、小红、小刚家
![]()
(2)解:小明家与小刚家相距:4﹣(﹣4.5)=8.5(千米)
(3)解:这辆货车此次送货共耗油:(4+1.5+10+4.5)×0.05=1(升).
答:小明家与小刚家相距8.5千米,这辆货车此次送货共耗油1升
【解析】(1)根据已知,以百货大楼为原点,以向东为正方向,用1个单位长度表示1千米一辆货车从百货大楼出发,向东走了4千米,到达小明家,继续向东走了1.5千米到达小红家,然后西走了8.5千米,到达小刚家,最后返回百货大楼,则小明家、小红家和小刚家在数轴上的位置可知.(2)用小明家的坐标减去与小刚家的坐标即可.(3)这辆货车一共行走的路程,实际上就是4+1.5+10+4.5=20(千米),货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程.
【考点精析】通过灵活运用正数与负数和数轴,掌握大于0的数叫正数;小于0的数叫负数;0既不是正数也不是负数;正数负数表示具有相反意义的量;数轴是规定了原点、正方向、单位长度的一条直线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
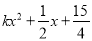 (k是常数).
(k是常数).(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=
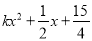 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;(3)若抛物线y=
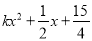 与x轴交于A(
与x轴交于A(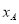 ,0)、B(
,0)、B(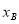 ,0)两点,且
,0)两点,且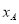 <
<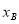 ,
, =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于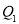 (
(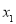 ,
,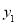 )、
)、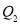 (
( ,
,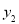 )两点,试探究
)两点,试探究 是否为定值,并写出探究过程.
是否为定值,并写出探究过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠1与∠2互为余角,∠1与∠3互为补角,那么下列结论: ①∠3﹣∠2=90° ②∠3+∠2=270°﹣2∠1 ③∠3﹣∠1=2∠2 ④∠3>∠1+∠2.
正确的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间7名工人日加工零件数分别为4,5,10,5,5,4,10则这组数据的众数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
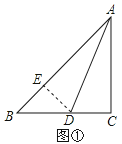
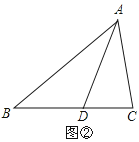

(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽做一道数学题:“已知两个多项式A,B,B为
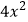 ﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是
﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是 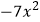 +10x+12.根据以上信息,你能求出A+B的结果吗?
+10x+12.根据以上信息,你能求出A+B的结果吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】一种细菌的半径约为0.000045米,用科学记数法表示为 米.
相关试题

