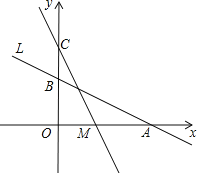
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
参考答案:
【答案】(1)A(4,0)、B(0,2);(2)0≤t≤4时,S△OCM=8﹣2t;t>4时,S△OCM=2t﹣8;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0)
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
(1)对于直线AB:y=﹣![]() x+2,
x+2,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
(3)∵OC=OA,∠AOB=∠COM=90°,
∴只需OB=OM,则△COM≌△AOB,
即OM=2,
此时,若M在x轴的正半轴时,t=2,
M在x轴的负半轴,则t=6.
故当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的函数值的范围是-11≤y≤9,求此函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的交点Q的纵坐标为4.
(1)求这两个函数的解析式;
(2)在同一直角坐标系中画出这两个函数的图象;
(3)求△PQO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式6-2(x+1)≤3(x-2).
(2)解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

(1)请在网格平面内作出平面直角坐标系;
(2)将△ABC平移至△DEF,使得A、B、C的对应点依次是D、E、F,已知D(2,3),请在网格中作出△DEF;
(3)若Q(a,b)是△DEF内一点,则△ABC内点Q的对应点点P的坐标是 (用a、b表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富学生课余生活,我校准备开设兴趣课堂.为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况,在全校进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果我校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
相关试题

