Question

【题目】已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动．

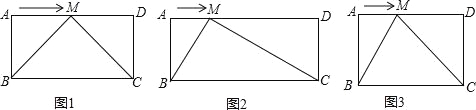
（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°；

（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC=90°，若存在，请给与证明；若不存在，请说明理由；

（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由．

Answer 1

【答案】（1）证明见解析（2）存在（3）不成立

【解析】

试题分析：（1）由b=2a，点M是AD的中点，可得AB=AM=MD=DC=a，又由四边形ABCD是矩形，即可求得∠AMB=∠DMC=45°，则可求得∠BMC=90°；

（2）由∠BMC=90°，易证得△ABM∽△DMC，设AM=x，根据相似三角形的对应边成比例，即可得方程：x2﹣bx+a2=0，由b＞2a，a＞0，b＞0，即可判定△＞0，即可确定方程有两个不相等的实数根，且两根均大于零，符合题意；

（3）由（2），当b＜2a，a＞0，b＞0，判定方程x2﹣bx+a2=0的根的情况，即可求得答案．

试题解析：（1）∵b=2a，点M是AD的中点，

∴AB=AM=MD=DC=a，

又∵在矩形ABCD中，∠A=∠D=90°，

∴∠AMB=∠DMC=45°，

∴∠BMC=90°．

（2）存在，

理由：若∠BMC=90°，

则∠AMB+∠DMC=90°，

又∵∠AMB+∠ABM=90°，

∴∠ABM=∠DMC，

又∵∠A=∠D=90°，

∴△ABM∽△DMC，

∴，

设AM=x，则，

整理得：x2﹣bx+a2=0，

∵b＞2a，a＞0，b＞0，

∴△=b2﹣4a2＞0，

∴方程有两个不相等的实数根，且两根均大于零，符合题意，

∴当b＞2a时，存在∠BMC=90°，

（3）不成立．

理由：若∠BMC=90°，

由（2）可知x2﹣bx+a2=0，

∵b＜2a，a＞0，b＞0，

∴△=b2﹣4a2＜0，

∴方程没有实数根，

∴当b＜2a时，不存在∠BMC=90°，即（2）中的结论不成立．