【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(6,3);(2)y=﹣x+6;(3)存在满足条件的点的P,其坐标为(6,0)或(3,﹣3)或(![]() ,
,![]() +6).
+6).
【解析】(1)把x=0,y=0分别代入直线L1,即可求出y和x的值,即得到B、C的坐标,解由直线BC和直线OA的方程组即可求出A的坐标;(2)设D(x,![]() x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
(1)解方程组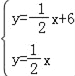 ,得
,得![]() , ∴A(6,3);
, ∴A(6,3);
(2)设D(x, ![]() x),
x),
∵△COD的面积为12,∴![]() ×6×x=12,
×6×x=12,
解得:x=4,∴D(4,2),
设直线CD的函数表达式是y=kx+b,
把C(0,6),D(4,2)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线CD解析式为y=﹣x+6;
(3)在直线l1:y=﹣![]() x+6中,当y=0时,x=12,
x+6中,当y=0时,x=12,
∴C(0,6)
存在点P,使以O、C、P、Q为顶点的四边形是菱形,
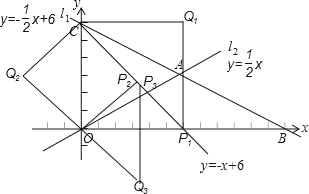
如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时OP1=OC=6,即P1(6,0);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到P2纵坐标为3,
把y=3代入直线直线CQ的解析式y=﹣x+6中,可得3=﹣x+6,解得x=3,此时P2(3,﹣3);
(iii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,设P3(x,﹣x+6),
∴x2+(﹣x+6﹣6)2=62,解得x=3![]() 或x=﹣3
或x=﹣3![]() (舍去),此时P3(3
(舍去),此时P3(3![]() ,﹣3
,﹣3![]() +6);
+6);
综上可知存在满足条件的点的P,其坐标为(6,0)或(3,﹣3)或(![]() ,
,![]() +6).
+6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地
所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地 如图
如图 是汽车行驶时离C站的路程
是汽车行驶时离C站的路程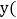 千米
千米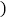 与行驶时间
与行驶时间 小时
小时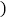 之间的函数关系的图象.
之间的函数关系的图象. 填空:
填空: ______km,AB两地的距离为______km;
______km,AB两地的距离为______km; 求线段PM、MN所表示的y与x之间的函数表达式;
求线段PM、MN所表示的y与x之间的函数表达式; 求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?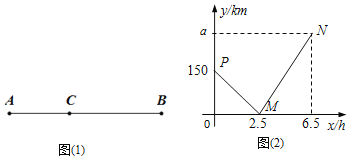
-
科目: 来源: 题型:
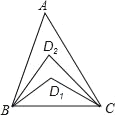
查看答案和解析>>【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数﹣3,1.
(1)在如图所示的数轴上,分别用A,B表示出﹣3,1这两个点;
(2)若|m|=2,数轴上表示m的点介于点A,B之间;在点A右侧且到点B距离为5的点表示的数为n.解关于x的不等式mx+4<n,并把解集表示在如图所示的数轴上.
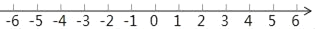
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小丽化简的过程,仔细阅读后解答所提出的问题.
解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a 第一步
=2ab﹣4a﹣1.第二步
(1)小丽的化简过程从第 步开始出现错误;
(2)请对原整式进行化简,并求当a=
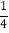 ,b=﹣6时原整式的值.
,b=﹣6时原整式的值. -
科目: 来源: 题型:
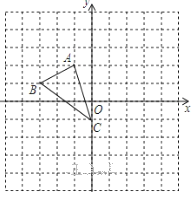
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
 作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标; 把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;(3)直接写出△A2B2C2的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形DEFG都是正方形,设AB=a,DE=b(a>b).
(1)写出AG的长度(用含字母a,b的代数式表示);
(2)观察图形,当用不同的方法表示图形中阴影部分的面积时,你能获得一个因式分解公式,请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2,试利用(2)中的公式,求a,b的值.
相关试题

