【题目】如图![]() 所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地
所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地![]() 如图
如图![]() 是汽车行驶时离C站的路程
是汽车行驶时离C站的路程![]() 千米
千米![]() 与行驶时间
与行驶时间![]() 小时
小时![]() 之间的函数关系的图象.
之间的函数关系的图象.
![]() 填空:
填空:![]() ______km,AB两地的距离为______km;
______km,AB两地的距离为______km;
![]() 求线段PM、MN所表示的y与x之间的函数表达式;
求线段PM、MN所表示的y与x之间的函数表达式;
![]() 求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
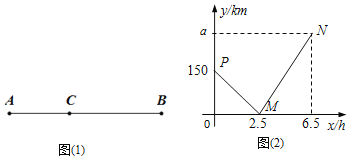
参考答案:
【答案】(1)240 390;(2)PM所表示的函数关系式为:![]() ,MN所表示的函数关系式为:
,MN所表示的函数关系式为:![]() ;(3)
;(3)![]() ,小汽车离车站C的路程不超过60千米.
,小汽车离车站C的路程不超过60千米.
【解析】
(1)根据图象中的数据即可得到A,B两地的距离;
(2)根据函数图象中的数据即可得到两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)根据题意可以分相遇前和相遇后两种情况进行解答.
解:![]() 由题意和图象可得,
由题意和图象可得,
![]() 千米,
千米,
A,B两地相距:![]() 千米,
千米,
故答案为:240,390
![]() 由图象可得,A与C之间的距离为150km
由图象可得,A与C之间的距离为150km
汽车的速度![]() ,
,
PM所表示的函数关系式为:![]()
MN所表示的函数关系式为:![]()
![]() 由
由![]() 得
得![]() ,解得:
,解得:![]()
由![]() 得
得![]() ,解得:
,解得:![]()
由图象可知当行驶时间满足:![]() ,小汽车离车站C的路程不超过60千米
,小汽车离车站C的路程不超过60千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
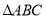 中,
中,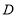 是
是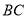 的中点,
的中点,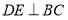 ,垂足为
,垂足为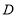 ,交
,交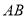 于点
于点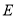 ,且
,且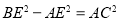 .
.(1)求
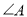 的度数;
的度数;(2)若
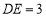 ,
,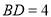 ,求
,求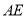 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
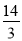 C.3D.
C.3D.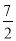
-
科目: 来源: 题型:
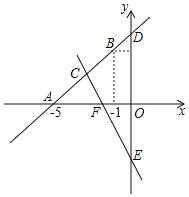
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.
-
科目: 来源: 题型:
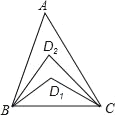
查看答案和解析>>【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数﹣3,1.
(1)在如图所示的数轴上,分别用A,B表示出﹣3,1这两个点;
(2)若|m|=2,数轴上表示m的点介于点A,B之间;在点A右侧且到点B距离为5的点表示的数为n.解关于x的不等式mx+4<n,并把解集表示在如图所示的数轴上.
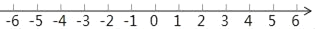
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:
 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.
交于点A.(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

相关试题

