【题目】某机动车出发前油箱内有油![]() ,行驶若干小时后,途中在加油站加油若干升.油箱中余油量
,行驶若干小时后,途中在加油站加油若干升.油箱中余油量![]() (
(![]() )与行驶时间
)与行驶时间![]() (
(![]() )之间的函数关系如图所示,根据图回答问题:
)之间的函数关系如图所示,根据图回答问题:

(1)机动车行驶![]() 后加油,途中加油 升:
后加油,途中加油 升:
(2)根据图形计算,机动车在加油前的行驶中每小时耗油多少升?
(3)如果加油站距目的地还有![]() ,车速为
,车速为![]() ,要到达目的地,油箱中的油是否够用?请说明理由.
,要到达目的地,油箱中的油是否够用?请说明理由.
参考答案:
【答案】(1)24;(2)每小时耗油量为6L;(3)油箱中的油不够用,理由见解析
【解析】
(1)图象上x=5时,对应着两个点,油量一多一少,可知此时加油多少;
(2)因为x=0时,Q=42,x=5时,Q=12,所以出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L;
(3)由图象知,加油后还可行驶6小时,即可行驶60×6千米,然后同400千米做比较,即可求出答案.
解:(1)由图可得,机动车行驶5小时后加油为3612=24;
故答案为:24;
(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,
因此每小时耗油量为6L,
(3)由图可知,加油后可行驶6h,
故加油后行驶60×6=360km,
∵400>360,
∴油箱中的油不够用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图(1),连接AF、CE.
①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题:

(1)汽车行驶h后加油,中途加油L;
(2)求加油前油箱剩余油量y与行驶时间x的函数解析式;
(3)若当油箱中剩余油量为10L时,油量表报警,提示需要加油,大巴车不再继续行驶,则该车最远能跑多远?此时,大巴车从出发到现在已经跑了多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.
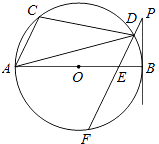
(1)判断直线BP和⊙O的位置关系,并说明你的理由;
(2)当⊙O的半径为 ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题发现:数学兴趣小组在活动时,老师提出了这样一个问题:如图①,在Rt△ABC中,∠BAC=90°,BC=10,AD是BC边上的中线,求AD的长度.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,则AD=
 AE
AE
在△ADC和△EDB中

∴△ADC≌△EDB
∴∠DBE=∠DCA,BE=AC
∴BE∥AC
∴∠EBA+∠BAC=180°
∵∠BAC=90°
∴∠EBA=90°
在△EBA和△CAB中

∴△EBA≌△CAB
∴AE=BC
∵BC=10
∴AD=
 AE=
AE= BC=5
BC=5(1)若将上述问题中条件“BC=10”换成“BC=a”,其他条件不变,则可得AD= .
从上得到结论:直角三角形斜边上的中线,等于斜边的一半.
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形进而求解.
问题解决:(2)如图②,在四边形ABCD中,AD∥BC,∠D=90°,M是AB的中点.若CM=6.5,BC+CD+DA=17,求四边形ABCD的面积.
问题拓展:(3)如图③,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,∠DFE与∠AEF的度数满足数量关系:∠DFE=k∠AEF,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.
(3)如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC,BC于点D,E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.
(4)问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
相关试题

