【题目】如图,在△ABC中,∠C=150°,AC=4,tanB= ![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.2)
=2.2)
参考答案:
【答案】
(1)解:过A作AD⊥BC,交BC的延长线于点D,如图1所示:

在Rt△ADC中,AC=4,
∵∠C=150°,
∴∠ACD=30°,
∴AD= ![]() AC=2,
AC=2,
CD=ACcos30°=4× ![]() =2
=2 ![]() ,
,
在Rt△ABD中,tanB= ![]() =
= ![]() =
= ![]() ,
,
∴BD=16,
∴BC=BD﹣CD=16﹣2 ![]() ;
;
(2)解:在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
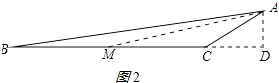
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD= ![]() =
= ![]() =
= ![]() =2﹣
=2﹣ ![]() ≈0.27≈0.3.
≈0.27≈0.3.
【解析】(1)由已知∠C=150°和tanB得值,添加辅助线构造直角三角形。过A作AD⊥BC,交BC的延长线于点D,利用锐角三角函数在Rt△ACD和在Rt△ABD中,求出相关线段的长,就可以求出结论。
(2)利用∠ACD=30°,根据外角构造15°的角,添加辅助线,在BC边上取一点M,使得CM=AC,连接AM,在Rt△AMD中,易求出AD、MD的长,利用锐角三角函数的定义即可求出tan15°的值。
【考点精析】通过灵活运用锐角三角函数的定义,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分
 ,BN
,BN AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
(1)求证:BN=DN;
(2)求MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
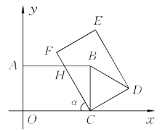
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,没有实数根的是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
A,B两种型号车的进货和销售价格表:A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
(1)求今年6月份A型车每辆销售价多少元;
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载)
B型车(满载)
运货总量
3辆
2辆
38吨
1辆
3辆
36吨
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知 ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形 的周长为___________.
的周长为___________.
相关试题

