【题目】已知:如图,点A、B分别是∠MON的边OM、ON上两点,OC平分∠MON,在∠CON的内部取一点P(点A、P、B三点不在同一直线上),连接PA、PB.
(1)探索∠APB与∠MON、∠PAO、∠PBO之间的数量关系,并证明你的结论;
(2)设∠OAP=x°,∠OBP=y°,若∠APB的平分线PQ交OC于点Q,求∠OQP的度数(用含有x、y的代数式表示).


参考答案:
【答案】(1)见解析;(2)∠OQP=180°+![]() x°﹣
x°﹣![]() y°或∠OQP=
y°或∠OQP=![]() x°﹣
x°﹣![]() y°.
y°.
【解析】【试题分析】(1)分下面两种情况进行说明;
①如图1,点P在直线AB的右侧,∠APB+∠MON+∠PAO+∠PBO=360°,
②如图2,点P在直线AB的左侧,∠APB=∠MON+∠PAO+∠PBO,
(2)分两种情况讨论,如图3和图4.
【试题解析】
(1)分两种情况:
①如图1,点P在直线AB的右侧,∠APB+∠MON+∠PAO+∠PBO=360°,
证明:∵四边形AOBP的内角和为(4﹣2)×180°=360°,
∴∠APB=360°﹣∠MON﹣∠PAO﹣∠PBO;

②如图2,点P在直线AB的左侧,∠APB=∠MON+∠PAO+∠PBO,
证明:延长AP交ON于点D,
∵∠ADB是△AOD的外角,
∴∠ADB=∠PAO+∠AOD,
∵∠APB是△PDB的外角,
∴∠APB=∠PDB+∠PBO,
∴∠APB=∠MON+∠PAO+∠PBO;
(2)设∠MON=2m°,∠APB=2n°,
∵OC平分∠MON,
∴∠AOC=![]() ∠MON=m°,
∠MON=m°,
∵PQ平分∠APB,
∴∠APQ=![]() ∠APB=n°,
∠APB=n°,
分两种情况:
第一种情况:如图3,∵∠OQP=∠MOC+∠PAO+∠APQ,即∠OQP=m°+x°+n°①
∵∠OQP+∠CON+∠OBP+∠BPQ=360°,
∴∠OQP=360°﹣∠CON﹣∠OBP﹣∠BPQ,即∠OQP=360°﹣m°﹣y°﹣n°②,
①+②得2∠OQP=360°+x°﹣y°,
∴∠OQP=180°+![]() x°﹣
x°﹣![]() y°;
y°;

第二种情况:如图4,∵∠OQP+∠APQ=∠MOC+∠PAO,
即∠OQP+n°=m°+x°,
∴2∠OQP+2n°=2m°+2x°①,
∵∠APB=∠MON+∠PAO+∠PBO,
∴2n°=2m°+x°+y°②,
①﹣②得2∠OQP=x°﹣y°,
∴∠OQP=![]() x°﹣
x°﹣![]() y°,
y°,
综上所述,∠OQP=180°+![]() x°﹣
x°﹣![]() y°或∠OQP=
y°或∠OQP=![]() x°﹣
x°﹣![]() y°.
y°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式x2-mx+n能因式分解为(x+2)(x-3),则m+n的值______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是它的外角和的2倍,则经过这个多边形的一个顶点最多可以画_____条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x、y满足2x+3y=1.
(1)用含有x的代数式表示y;
(2)若实数y满足y>1,求x的取值范围;
(3)若实数x、y满足x>﹣1,y≥﹣
 ,且2x﹣3y=k,求k的取值范围.
,且2x﹣3y=k,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
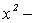 mx-3x+m-4=0(m为常数).
mx-3x+m-4=0(m为常数).(1)求证:方程有两个不相等的实数根;
(2)设
 ,
,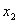 是方程的两个实数根,且
是方程的两个实数根,且 +
+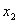 =6.请求出方程的这两个实数根.
=6.请求出方程的这两个实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:

(1)写出用含x、y的代数式表示厨房的面积是________m2;卧室的面积是________m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=2,xy=-1,则x2+y2=______.
相关试题

