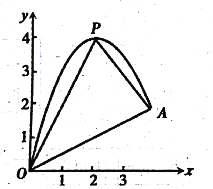
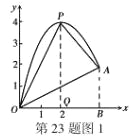
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标。
参考答案:
【答案】(1)、P(2,4);(2)、A(![]() ,
,![]() );(3)、
);(3)、![]() ;(4)、M(
;(4)、M(![]() ,
,![]() ).
).
【解析】
试题分析:(1)、利用配方法将二次函数配成顶点式,从而得出点P的坐标;(2)、将二次函数和一次函数联立成方程组,从而求出点的坐标;(3)、作PQ⊥x轴于点Q,AB⊥x轴于点B,根据△AOP的面积=△POQ的面积+梯形PQBA的面积-△AOB的面积得出答案;(4)、过P作OA的平行线,交抛物线于点M,连接OM、AM,得出△MOA的面积等于△POA的面积,设直线PM的解析式为y=![]() x+b,将点P坐标代入得出解析式,然后与二次函数联立成方程组得出答案.
x+b,将点P坐标代入得出解析式,然后与二次函数联立成方程组得出答案.
试题解析:(1)、由题意得:y=-![]() +4x=-
+4x=-![]() +4 ∴点P的坐标为(2,4)
+4 ∴点P的坐标为(2,4)
(2)、联立两解析式可得: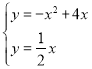 解得:
解得:![]() 或
或![]()
∴点A的坐标为(![]() ,
,![]() )
)
(3)、如图1,作PQ⊥x轴于点Q,AB⊥x轴于点B
![]() =
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() -2)-
-2)-![]() ×
×![]() ×
×![]() =4+
=4+![]() -
-![]() =
=![]() .
.
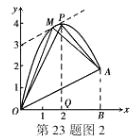
(4)、如图2,过P作OA的平行线,交抛物线于点M,连接OM、AM,则△MOA的面积等于△POA的面积
设直线PM的解析式为:y=![]() x+b ∵点P的坐标为(2,4) ∴b=3
x+b ∵点P的坐标为(2,4) ∴b=3
∴直线PM的解析式为:y=![]() x+3
x+3
由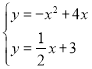 解得:
解得:![]() 或
或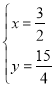 ∴点M的坐标为:(
∴点M的坐标为:(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角? (填“是”或“不是”).
小丽经过三次折叠发现了∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图:
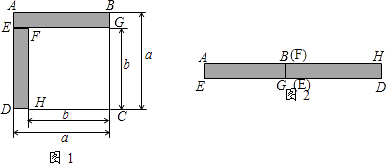
(1)如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和EFHD为阴影部分,则阴影部分的面积是(写成平方差的形式)
(2)将图1中的长方形ABGE和EFHD剪下来,拼成图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式)
(3)比较图1与图2的阴影部分的面积,可得乘法公式 .
(4)利用所得公式计算:2(1+ )(1+
)(1+ 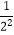 )(1+
)(1+ 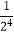 )(1+
)(1+ 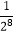 )+
)+ 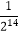 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正数x的两个平方根分别为3﹣a和2a+7.
(1)求a的值;
(2)求44﹣x这个数的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动,记△ABP的面积为t(cm2),y与运动时间t(s)的关系如图2所示.
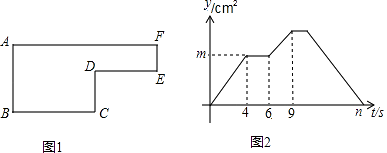
若AB=6cm,请回答下列问题:
(1)求图1中BC、CD的长及边框所围成图形的面积;
(2)求图2中m、n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位数比十位数字大4,而且这个两位数比它的数字之和的3倍大2,则这个两位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
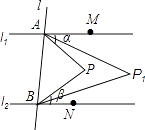
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
相关试题

