搜索
【题目】如下图：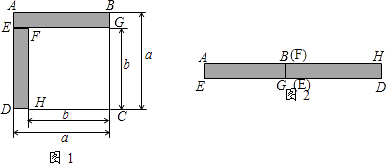 
（1）如图1，已知正方形ABCD的边长为a，正方形FGCH的边长为b，长方形ABGE和EFHD为阴影部分，则阴影部分的面积是（写成平方差的形式）
（2）将图1中的长方形ABGE和EFHD剪下来，拼成图2所示的长方形，则长方形AHDE的面积是（写成多项式相乘的形式）
（3）比较图1与图2的阴影部分的面积，可得乘法公式 ．
（4）利用所得公式计算：2（1+ 
）（1+ 
）（1+ 
）（1+ 
）+ 
．
参考答案：
【答案】
（1）a2﹣b2
（2）（a+b）（a﹣b）
（3）（a+b）（a﹣b）=a2﹣b2
（4）解：原式=4（1﹣ 
）（1+ ）（1+ 
）（1+ 
）（1+ 
）+ 
=4（1﹣ ）（1+ ）（1+ ）（1+ ）+
=4（1﹣ ）（1+ ）（1+ ）+
=4（1﹣ ）（1+ ）+
=4（1﹣ 
）+
=4﹣ +
=4．
【解析】解：（1）根据题意得：阴影部分面积为a2﹣b2；（2）根据题意得：阴影部分面积为（a+b）（a﹣b）；（3）可得（a+b）（a﹣b）=a2﹣b2； 所以答案是：（1）a2﹣b2；（2）（a+b）（a﹣b）；（3）（a+b）（a﹣b）=a2﹣b2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D，F在线段AB上，点E，G分别在线段BC和AC上，CD∥EF，∠1=∠2．
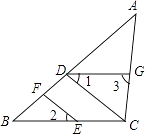
（1）判断DG与BC的位置关系，并说明理由；
（2）若DG是∠ADC的平分线，∠3=85°，且∠DCE：∠DCG=9：10，试说明AB与CD有怎样的位置关系？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数y=
（k≠o）的图象在第一象限交于点C，如果点B的坐标为(0，2)．OA=OB，B是线段AC的中点．(l)求点A的坐标及一次函数解析式；
(2)求点C的坐标及反比例函数的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解
如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
探究发现
△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ （填“是”或“不是”）．
小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
应用提升
（3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．
-
科目： 来源： 题型：
查看答案和解析>>【题目】正数x的两个平方根分别为3﹣a和2a+7．
（1）求a的值；
（2）求44﹣x这个数的立方根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一小球从斜坡D点处抛出，球的抛出路线可以用二次函数）y=-x2+4x刻画，斜坡OA可以用一次函数y=
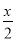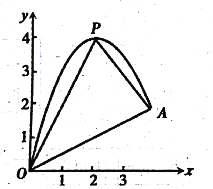
刻画．(1)请用配方法求二次函数图象的最高点P的坐标；
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
(4)在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积，请直接写出点M的坐标。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动，记△ABP的面积为t（cm2），y与运动时间t（s）的关系如图2所示．
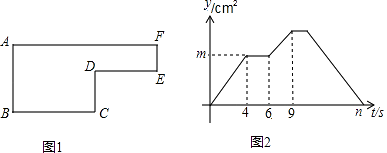
若AB=6cm，请回答下列问题：
（1）求图1中BC、CD的长及边框所围成图形的面积；
（2）求图2中m、n的值．
相关试题
