【题目】已知矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD,垂足为E,AD=8,
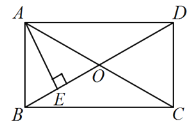
(1)若∠DAE︰∠BAE=3︰1,求∠EAC的度数;
(2)若ED=3BE,求AE的长.
参考答案:
【答案】(1)45°;(2)4.
【解析】
(1)由已知条件求出∠BAE=22.5°,再根据矩形的性质得到OA=OB,求出∠OAB=∠ABE=67.5°,即可得出∠EAC的度数;
(2)根据矩形的性质和等腰三角形三线合一的性质得到△OAB是等边三角形,求出∠ADE =30°,利用含30°角的直角三角形的性质可求出AE.
(1)解:∵∠DAE︰∠BAE=3︰1,
∴∠BAE=90°×![]() =22.5°,
=22.5°,
∴∠ABE=67.5°,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO
∴OA=OB,
∴∠OAB=∠ABE=67.5°
∴∠EAC=∠OAB![]() ∠BAE=67.5°
∠BAE=67.5°![]() 22.5°=45°;
22.5°=45°;
(2)∵OA=OB=OD,ED=3BE,
∴OE+OD=3BE,
∴OB![]() BE+OB=3BE,
BE+OB=3BE,
∴OB =2BE,
∴点E为OB的中点,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,即△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°![]() ∠ABD=30°,
∠ABD=30°,
∵AE⊥BD,AD=8,
∴AE=![]() AD=4.
AD=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,
(1)问应将每件售价定为多少元时,才能使每天利润为640元且成本最少?
(2)问应将每件售价定为多少元时,才能使每天利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
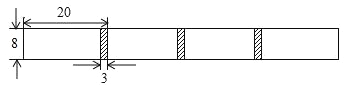
 根据题意,将下面的表格补充完整:
根据题意,将下面的表格补充完整:白纸张数
 张
张
1
2
3
4
5

纸条长度
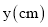
20
______
54
71
______

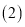 直接写出用x表示y的关系式:______ ;
直接写出用x表示y的关系式:______ ; 要使粘合后的总长度为1006cm,需用多少张这样的白纸?
要使粘合后的总长度为1006cm,需用多少张这样的白纸? -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].

(1)、如图①,对△ABC作变换[50°,
 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
-
科目: 来源: 题型:
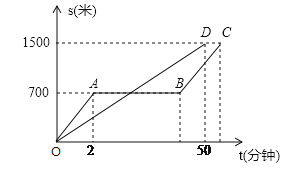
查看答案和解析>>【题目】“龟免赛跑”的故事同学们都非常热悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中_______(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是___________米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来假,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AC=4cm,BC=3cm,点P由B出发沿BA的方向向点A匀速运动,速度为1cm/s,同时点Q由A出发沿AC的方向向点C匀速运动,速度为2cm/s,连接PQ,设运动的时间为t(s),其中0<t<2,解答下列问题:

(1)当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,线段PQ将△ABC的面积分成1:2两部分?若存在,求出此时的t,若不存在,请说明理由;
(3)点P、Q在运动的过程中,△CPQ能否成为等腰三角形?若能,请求出此时t的值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.已知:在矩形
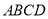 中,
中,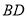 是对角线,
是对角线,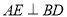 于点
于点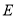 ,
,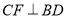 于点
于点 ;
;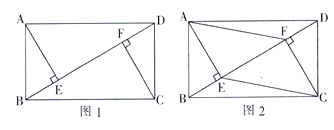
(1)如图1,求证:
 ;
;(2)如图2,当
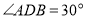 时,连接
时,连接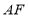 .
.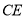 ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形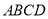 面积的
面积的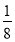 .
.
相关试题

