搜索
【题目】如图，已知C是AB的中点，D是AC的中点，E是BC的中点．
(1)若DE=9cm，求AB的长.
(2)若CE=5cm，求DB的长．
参考答案：
【答案】（1）AB=18；（2）DB=15.
【解析】
（1）由线段中点的定义可得CD=
AC，CE=BC，根据线段的和差关系可得DE=AB，进而可得答案；（2）根据中点定义可得AC=BC，CE=BE，AD=CD，根据线段的和差关系即可得答案.
（1）∵D是AC的中点，E是BC的中点．
∴CD=AC，CE=BC，
∵DE=CD+CE=9，
∴AC+BC=(AC+BC)=9，
∵AC+BC=AB，
∴AB=18.
（2）∵C是AB的中点，D是AC的中点，E是BC的中点，
∴AC=BC，CE=BE=BC，，AD=CD=AC，
∴AD=CD=CE=BE，
∴DB=CD+CE+BE=3CE，
∵CE=5，
∴DB=15.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是平行四边形，点A（1，0），B（4，1），C（4，3），反比例函数y=
的图象经过点D，点P是一次函数y=mx+3﹣4m（m≠0）的图象与该反比例函数图象的一个公共点；（1）求反比例函数的解析式；
（2）通过计算说明一次函数y=mx+3﹣4m的图象一定过点C；
（3）对于一次函数y=mx+3﹣4m（m≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围，（不必写过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：
（1）求证：△BEF∽△DCB；
（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；
（3）如图2过点Q作QG⊥AB，垂足为G，当t为何值时，四边形EPQG为矩形，请说明理由；
（4）当t为何值时，△PQF为等腰三角形？试说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上点O为原点，A点表示数a，B点表示数b，且a、b满足|a+2|+|b-4|=0；
(1)点A表示的数为 ；点B表示的数为 ；
(2)如果M、N为数轴上两个动点.点M从点A出发，速度为每秒1个单位长度；点N从点B出发，速度为点A的3倍，它们同时向左运动.
①当运动2秒时，点M、N对应的数分别是 、 .
②当运动t秒时，点M、N对应的数分别是 、 .(用含t的式子表示)
③运动多少秒时，点M、N、O中恰有一个点为另外两个点所连线段的中点？(可以直接写出答案)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C在线段AB上，点M、N分别是AC、BC的中点．
若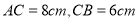
，求线段MN的长；
若C为线段AB上任一点，满足
，其它条件不变，你能猜想MN的长度吗？并说明理由，你能用一句简洁的话描述你发现的结论吗？
若C在线段AB的延长线上，且满足
cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l上有三点A、B、C，AB=3，AC=2，点M是AC的中点.
(1)根据条件，画出图形；
(2)求线段BM的长.
-
科目： 来源： 题型：
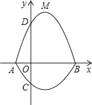
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣
），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求m的值．
相关试题
