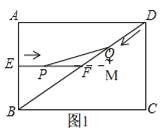
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.

参考答案:
【答案】(1)证明见解析(2)![]() 或2(3)t=1或3或
或2(3)t=1或3或![]() 或
或![]() 秒时,△PQF是等腰三角形
秒时,△PQF是等腰三角形
【解析】试题分析:![]() 两组角对应相等,两三角形相似.
两组角对应相等,两三角形相似.
![]() 过点
过点![]() 作
作![]() 于
于![]() ,得出
,得出![]() 把
把![]() 用
用![]() 表示出来,即可表示出
表示出来,即可表示出![]() 的面积,求出
的面积,求出![]() 即可.
即可.
![]() 四边形
四边形![]() 为矩形时,
为矩形时,![]() 对应边的比相等,即可求出
对应边的比相等,即可求出![]() 得值.
得值.
![]() 分成四种情况进行讨论.
分成四种情况进行讨论.
试题解析:(1)∵四边形![]() 是矩形,
是矩形,
![]()
在![]() 中,
中,![]()
![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
(2)如图1,过点![]() 作
作![]() 于
于![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() (舍)或
(舍)或![]() 秒;
秒;
![]() 四边形
四边形![]() 为矩形时,如图所示:
为矩形时,如图所示:

![]()
![]()
![]()
解得:![]()
![]() 当点
当点![]() 在
在![]() 上时,如图2,
上时,如图2,![]()

![]()
![]()
当点![]() 在
在![]() 上时,
上时,![]() 如图3,
如图3,

![]()
![]()
![]() 时,如图4,
时,如图4,

![]()
![]()
![]() 时,如图5,
时,如图5,

![]()
![]()
综上所述,![]() 或
或![]() 或
或![]() 或
或![]() 秒时,
秒时,![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
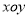 中,已知点
中,已知点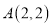 ,
,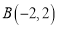 ,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________.
,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在矩形ABCD内,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作矩形”的尺规作图过程,已知:
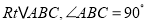
求作:矩形
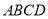
作法:如图,
①作线段
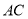 的垂直平分线角交
的垂直平分线角交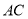 于点
于点 ;
;②连接
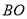 并延长,在延长线上截取
并延长,在延长线上截取
③连接
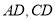
所以四边形
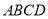 即为所求作的矩形
即为所求作的矩形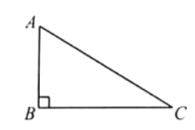
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:
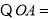 ,
, ,
, 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)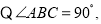
 四边形
四边形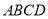 是矩形( )(填推理的依据)
是矩形( )(填推理的依据) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:
 (1)本次接受问卷调查的同学有多少人?补全条形统计图.
(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道数学中的整体思想吗?解题中,若把注意力和着眼点放在问题的整体上,多方位思考、联想、探究,进行整体思考、整体加减,能使问题迅速获解.
例题:已知x2+xy=4,xy+y2=-1.求代数式x2-y2的值.
解:将两式相减,得(x2+xy)-(xy+y2)=4-(-1),即x2-y2=5;请用整体思想解答下列问题:
(1)在例题的基础上求(x+y)2的值;
(2)若关于x、y的二元一次方程组
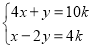 的解也是二元一次方程x+y=6的解,求k的值.
的解也是二元一次方程x+y=6的解,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h)
路程(km)
时间(h)
大巴车
x
120
________
小汽车
________
120
________
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
相关试题

