【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.

参考答案:
【答案】(1)AB∥CD,理由见解析;(2)证明见解析;(3)45°.
【解析】
(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;
(2)利用(1)中平行线的性质推知∠BEF+∠EFD=180°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;
(3)利用三角形外角定理、三角形内角和定理求得![]() ;然后由邻补角的定义、角平分线的定义推知
;然后由邻补角的定义、角平分线的定义推知![]() ;最后根据图形中的角与角间的和差关系求得∠HPQ=45°.
;最后根据图形中的角与角间的和差关系求得∠HPQ=45°.
(1)AB∥CD,
理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴![]()
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH;
(3)∵∠PHK=∠HPK,
∴∠PKG=2∠HPK.
又∵GH⊥EG,
∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,
∴∠EPK=180°﹣∠KPG=90°+2∠HPK.
∵PQ平分∠EPK,
∴![]() ,
,
∴∠HPQ=∠QPK﹣∠HPK=45°.
答:∠HPQ的度数为45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,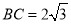 ,
, ,
, 、
、 分别是
分别是 、
、 上的点,且
上的点,且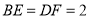 ,连结
,连结 、
、 .点
.点 是线段
是线段 上的点,过点
上的点,过点 作
作 交
交 于点
于点 ,设AP=x.
,设AP=x.
(1)求证:四边形
 是菱形;
是菱形;(2)用含
 的代数式表示
的代数式表示 的长;
的长;(3)连结
 ,当
,当 为何值时
为何值时 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据语句画图,并回答问题,如图,∠AOB内有一点P.
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D.
(2)写出图中与∠CPD互补的角 .(写两个即可)
(3)写出图中∠O相等的角 .(写两个即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为
 ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为A. 6、7B. 7、8C. 6、7、8D. 6、8、9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值.
相关试题

