Question

【题目】已知：如图，AB=AC，AD=AE，∠BAC=∠DAE=α，BE与AC、CD分别相交于点N、M.

（1）求证：BE=CD；

（2）求∠BMC的大小.（用α表示）

Answer 1

【答案】（1）详见解析；（2）α.

【解析】试题分析：（1）先由∠BAC=∠DAE得出∠BAE=∠CAD，再由边角边证三角形全等，对应边相等即可；

（2）由全等三角形的性质得出∠B=∠C，又由对顶角相等及三角形内角和定理即可求得∠BMC.

试题解析：（1）∵∠BAC=∠DAE，

∴∠BAC+∠CAE=∠DAE+∠CAE，

即∠BAE=∠CAD,

在△BAE与△CAD中, ，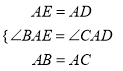

∴△BAE≌△CAD，（SAS）

∴BE=CD.

（2）∵△BAE≌△CAD，

∴∠B=∠C,

∵∠ANB=∠MNC,

∴∠BMC=∠BAC=α.