【题目】如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm．矩形ABCD的边AD，AB分别与l1，l2重合，AB＝cm，AD＝4cm．若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为3cm/s，矩形ABCD的移动速度为4cm/s，设移动时间为t(s)．

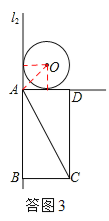
(1)如图①，连接OA，AC，则∠OAC的度数为 °；

(2)如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离(即OO1的长）；

(3)在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d(cm)．当d<2时，求t的取值范围．（解答时可以利用备用图画出相关示意图）

参考答案：

【答案】（1）105；（2）；（3）＜t＜.

【解析】试题分析：（1）⊙O与l1，l2都相切，连接圆心和两个切点，等正方向.OA即为正方形的对角线，得到∠OAD=450，再在Rt△ADC中，由锐角三角函数求∠DAC=600，从而求得∠OAC的度数1050.

（2）连接O1与切点E，则O1E=2，O1E⊥l1，利用△O1EA1∽△D1C1E1,求A1E=，根据2+O1O+A1E=AA1，可求t，进而求得圆心移动的距离3t=.

（3）圆心O到对角线AC的距离d＜2，即d＜r.说明⊙O与AC相交，所以出找两个临界点的t值，即⊙O与AC相切．运动中存在两个相切的位置.分别求两个相切时t的值，即可得出d＜r时，t的取值

试题解析：解：（1）1050.

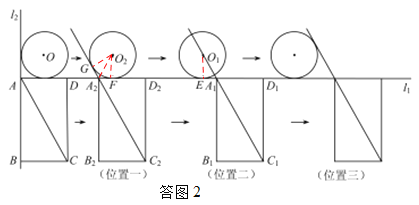
（2）O1，A1，C1恰好在同一直线上时，设⊙O与AC的切点为E，连接O1E，如答图1，

可得O1E=2，O1E⊥l1，

在Rt△A1D1C1中，∵A1D1=4，D1C1=，

∴tan∠C1A1D1=．∴∠C1A1D1=600．

在Rt△A1O1E中, ∠O1A1E=∠C1A1D1=600．∴A1E=,

∵，∴，∴.

∴OO1=3t=.

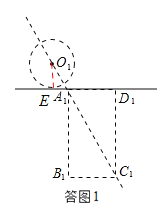
（3）如答图2，

①当直线AC与⊙O第一次相切时，设移动时间为t1.如位置一，此时⊙O移动到⊙O2的位置，矩形ABCD移动到A2B2C2D2的位置.

设⊙O2与直线l1、A2C2分别相切于点F、G, 连接O2F、O2G、O2A2，

∴O2F⊥l1、O2G⊥A2C2.

又由（2）可得∠C2A2D2=600于，∴∠GA2F=1200．∴∠O2A2F=600.

在Rt△O2A2F中，O2F=2，∴A2F=.

∵OO2=3t1， ，∴，解得.

②当点O1，A1，C1恰好在同一直线上时为位置二，设移动时间为t2.由（2）可得.

③当直线AC与⊙O第二次相切时，设移动时间为t3．如位置3，由题意知，从位置一到位置二所用时间与位置二到位置三所用时间相等.

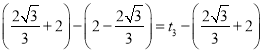∴，即，解得.

综上所述，当d<2时，t的取值范围为＜t＜.

关闭