【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() (点
(点 ![]() 分别在
分别在 ![]() 轴的左右两侧)两点,与
轴的左右两侧)两点,与 ![]() 轴的正半轴交于点
轴的正半轴交于点 ![]() ,顶点为
,顶点为 ![]() ,已知点
,已知点 ![]() .
.
(1)求点 ![]() 的坐标;
的坐标;
(2)判断△ ![]() 的形状,并说明理由;
的形状,并说明理由;
(3)将△ ![]() 沿
沿 ![]() 轴向右平移
轴向右平移 ![]() 个单位(
个单位( ![]() )得到△
)得到△ ![]() .△
.△ ![]() 与△
与△ ![]() 重叠部分(如图中阴影)面积为
重叠部分(如图中阴影)面积为 ![]() ,求
,求 ![]() 与
与 ![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】
(1)解:如答题1所示:

∵点A(-1,0)在抛物线y=-(x-1)2+c上,
∴0=-(-1-1)2+c,得c=4,
∴抛物线解析式为:y=-(x-1)2+4,
令x=0,得y=3,∴C(0,3);
令y=0,得x=-1或x=3,∴B(3,0).
(2)解:△CDB为直角三角形.理由如下:
由抛物线解析式,得顶点D的坐标为(1,4).
如答图1所示,过点D作DM⊥x轴于点M,则OM=1,DM=4,BM=OB-OM=2.
过点C作CN⊥DM于点N,则CN=1,DN=DM-MN=DM-OC=1.
在Rt△OBC中,由勾股定理得:BC= ![]() ;
;
在Rt△CND中,由勾股定理得:CD= ![]() ;
;
在Rt△BMD中,由勾股定理得:BD= ![]() .
.
∵BC2+CD2=BD2,
∴△CDB为直角三角形(勾股定理的逆定理)
(3)解:设直线BC的解析式为y=kx+b,∵B(3,0),C(0,3),
∴ ![]() ,
,
解得k=-1,b=3,
∴y=-x+3,
直线QE是直线BC向右平移t个单位得到,
∴直线QE的解析式为:y=-(x-t)+3=-x+3+t;
设直线BD的解析式为y=mx+n,∵B(3,0),D(1,4),
∴ ![]() ,
,
解得:m=-2,n=6,
∴y=-2x+6.
连接CQ并延长,射线CQ交BD于点G,则G( ![]() ,3).
,3).
在△COB向右平移的过程中:
(I)当0<t≤ ![]() 时,如答图2所示:
时,如答图2所示:

设PQ与BC交于点K,可得QK=CQ=t,PB=PK=3-t.
设QE与BD的交点为F,则:
![]() ,解得
,解得 ![]() ,
,
∴F(3-t,2t).
S=S△QPE-S△PBK-S△FBE= ![]() PEPQ-
PEPQ- ![]() PBPK-
PBPK- ![]() BEyF=
BEyF= ![]() ×3×3-
×3×3- ![]() (3-t)2-
(3-t)2- ![]() t2t=-
t2t=- ![]() t2+3t;
t2+3t;
(II)当 ![]() <t<3时,如答图3所示:
<t<3时,如答图3所示:

设PQ分别与BC、BD交于点K、点J.
∵CQ=t,
∴KQ=t,PK=PB=3-t.
直线BD解析式为y=-2x+6,令x=t,得y=6-2t,
∴J(t,6-2t).
S=S△PBJ-S△PBK= ![]() PBPJ-
PBPJ- ![]() PBPK=
PBPK= ![]() (3-t)(6-2t)-
(3-t)(6-2t)- ![]() (3-t)2=
(3-t)2= ![]() t2-3t+
t2-3t+ ![]() .
.
综上所述,S与t的函数关系式为:
S=  .
.
【解析】(1)首先用待定系数法,将点A的坐标代入函数解析式,求出c的值,就可以求出抛物线的解析式,然后由x=0,求出函数值,得到点C的坐标,由y=0,建立方程求出自变量的值,得到点B的坐标。
(2)利用勾股定理分别求出△CDB三边的平方,利用勾股定理的逆定理,求较小两边的平方和是否等于最大边的平方,判定△CDB为直角三角形。
(3)先分别求出直线BC的解析式、直线QE的解析式、直线BD的解析式及点G的坐标。△COB沿x轴向右平移过程中,分两个阶段:当0<t≤![]() 时,如图2所示,此时重叠部分为一个四边形,根据S=S△QPE-S△PBK-S△FBE,即可求出结果;当
时,如图2所示,此时重叠部分为一个四边形,根据S=S△QPE-S△PBK-S△FBE,即可求出结果;当 ![]() <t<3时,如答图3所示,根据S=S△PBJ-S△PBK,即可求出结果。
<t<3时,如答图3所示,根据S=S△PBJ-S△PBK,即可求出结果。
【考点精析】本题主要考查了确定一次函数的表达式和勾股定理的逆定理的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,AB为⊙O的直径,AC是弦,
 ,
,  .
.
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD = ∠E.

-
科目: 来源: 题型:
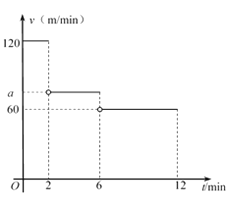
查看答案和解析>>【题目】小明从家出发,沿一条直道散步到离家450 m的邮局,经过一段时间原路返回,刚好在第12 min回到家中.设小明出发第t min时的速度为v m/min,v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第2 min时离家的距离为 m;
(2)当2< t ≤6时,求小明的速度a;
(3)求小明到达邮局的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.65
1.4
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n(n═1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
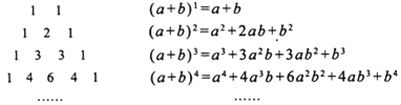
请依据上述规律,写出(x﹣2)2018展开式中含x2017项的系数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(数学阅读)
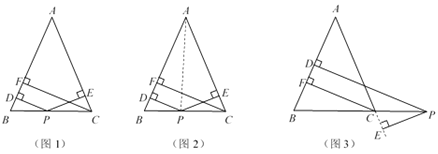
如图1,在△ABC中,AB=AC,点P为边BC上的任意一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
小尧的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
(推广延伸)
如图3,当点P在BC延长线上时,其余条件不变,请运用上述解答中所积累的经验和方法,猜想PD,PE与CF的数量关系,并证明.
(解决问题)
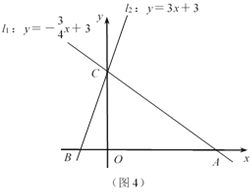
如图4,在平面直角坐标系中有两条直线l1:y=-
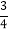 x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.(1)两条直线的交点C的坐标为 ;
(2)说明△ABC是等腰三角形;
(3)若l2上的一点M到l1的距离是1,运用上面的结论,求点M的坐标.
相关试题

