【题目】在⊙O中,AB为⊙O的直径,AC是弦, ![]() ,
, ![]() .
.
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当 ![]() 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
参考答案:
【答案】
(1)解:∵CP与⊙O相切,OC是半径.
∴CP⊥OC,
又∵∠OAC=∠AOC=60°,
∴∠P=90°-∠AOC=30°,
∴在Rt△POC中,CO= ![]() PO=4,
PO=4,
则PO=2CO=8
(2)解:如图,
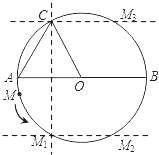
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°∴当点M运动到M1时,S△MAO=S△CAO,
此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ;
;
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.
∴∠AOM1=∠M1OM2=∠BOM2=60°
∴ ![]() 或
或 ![]() ,
,
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]() π;
π;
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO
∴∠BOM3=60°,
∴ ![]() =
= ![]() ×240或
×240或 ![]() =
= ![]() ×2=
×2= ![]()
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]() ;
;
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为 ![]() ×300°或
×300°或 ![]() π+
π+ ![]() =
= ![]()
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]()
【解析】(1)根据CP与⊙O相切,得出CP⊥OC,根据题意易证△OAC是等边三角形,可求出∠P=30°,再根据直角三角形中,30°的直角边等于斜边的一半,求出OP的长。
(2)如图,当S△MAO=S△CAO时,动点M的位置有四种.①作点C关于直径AB的对称点M1,连接AM1,OM1,先证S△MAO=S△CAO,再求出点M经过的弧长,即可求出半径OM所扫过的扇形的面积;②过点M1作M1M2∥AB交 O于点M2,连接AM2,OM2,③过点C作CM3∥AB交 O于点M3,连接AM3,OM3;④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得点M经过的弧长,然后求出半径OM所扫过的扇形的面积。
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )

A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上 A点表示的数是 a ,B 点表示的数是b ,且 ab满足|a 8|b-220.动线段 CD=4(点 D 在点 C 的右侧),从点 C与点 A重合的位置出发,以每秒 2 个单位的速度向右运动,运动时间为 t秒.
(1)求a,b的值, 运动过程中,点 D 表示的数是多少,(用含有 t 的代数式表示)
(2)在 B、C、D 三个点中,其中一个点是另外两个点为端点的线段的中点,求 t 的值;
(3)当线段 CD 在线段 AB上(不含端点重合)时,如图,图中所有线段的和记作为 S, 则 S的值是否随时间 t 的变化而变化?若变化,请说明理由;若不变,请求出 S值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的三个顶点A、B、D分别在长方形 EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为
 ,
, ,则正方形ABCD的面积为______.
,则正方形ABCD的面积为______. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD = ∠E.

-
科目: 来源: 题型:
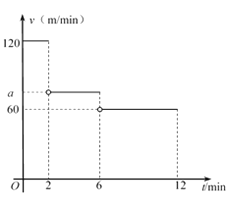
查看答案和解析>>【题目】小明从家出发,沿一条直道散步到离家450 m的邮局,经过一段时间原路返回,刚好在第12 min回到家中.设小明出发第t min时的速度为v m/min,v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第2 min时离家的距离为 m;
(2)当2< t ≤6时,求小明的速度a;
(3)求小明到达邮局的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与  轴交于点
轴交于点  (点
(点  分别在
分别在  轴的左右两侧)两点,与
轴的左右两侧)两点,与  轴的正半轴交于点
轴的正半轴交于点  ,顶点为
,顶点为  ,已知点
,已知点  .
.
(1)求点 的坐标;
的坐标;
(2)判断△ 的形状,并说明理由;
的形状,并说明理由;
(3)将△ 沿
沿  轴向右平移
轴向右平移  个单位(
个单位(  )得到△
)得到△  .△
.△  与△
与△  重叠部分(如图中阴影)面积为
重叠部分(如图中阴影)面积为  ,求
,求  与
与  的函数关系式,并写出自变量
的函数关系式,并写出自变量  的取值范围.
的取值范围.
相关试题

