【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为A、B、C、D四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)求本次被抽查的学生共有多少人?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“A”所在扇形圆心角的度数;
(4)估计全校“D”等级的学生有多少人?
参考答案:
【答案】
(1)解:12÷20%=60(人)
(2)解:B所占的百分比是: ![]() ×100%=40%,
×100%=40%,
D所占的百分比是:1﹣20%﹣40%﹣30%=10%.
C的个数是:60×30%=18,
D的个数是:60×10%=6.

(3)解:360°×20%=72°
(4)解:1200×10%=120(人).
答:估计全校“D”等级的学生有120人.
【解析】(1)部分÷百分比=总量;(3)扇形圆心角=360°×百分比;(4)样本中的百分比可以估计总体中的百分比.
【考点精析】掌握扇形统计图和条形统计图是解答本题的根本,需要知道能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是 =
=  =
=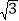 ;
;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学
 元购进甲、乙两种医用口罩共计
元购进甲、乙两种医用口罩共计 盒,甲,乙两种口罩的售价分别是
盒,甲,乙两种口罩的售价分别是 元/盒,
元/盒, 元/盒;甲,乙两 种口罩的数量分别是
元/盒;甲,乙两 种口罩的数量分别是 个/盒,
个/盒, 个/盒.
个/盒. (1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计
 人,每人每天
人,每人每天 个口罩,问购买的口罩数量是否能满足教育局的要求?
个口罩,问购买的口罩数量是否能满足教育局的要求? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).

(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 画出△A2B2C2 , 并直接写出S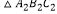 :S
:S  = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,将
,将 沿
沿 平移,且使
平移,且使 点平移到
点平移到 点,
点, 平移后的对应点分别为
平移后的对应点分别为 .
. 
(1)写出
 两点的坐标;
两点的坐标; (2)画出平移后所得的
 ;
;(3)五边形
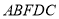 的面积
的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算

(2)解不等式组
 ,并写出不等式组的非负整数解。
,并写出不等式组的非负整数解。(3)解分式方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义一种新运算T,规定:T(x,y)=
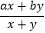 (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=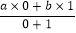 =b,已知T(1,1)=2.5,T(4,﹣2)=4.
=b,已知T(1,1)=2.5,T(4,﹣2)=4.(1)求a,b的值;
(2)若关于m的不等式组
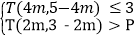 恰好有2个整数解,求实数P的取值范围.
恰好有2个整数解,求实数P的取值范围.
相关试题

