Question

【题目】问题背景：如图1，等腰△ABC中，AB=AC，∠BAC=120°，作AD⊥BC于点D，则D为BC的中点，∠BAD=∠BAC=60°，于是 = =；

迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，D，E，C三点在同一条直线上，连接BD．

①求证：△ADB≌△AEC；

②请直接写出线段AD，BD，CD之间的等量关系式；

拓展延伸：如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF．

①证明△CEF是等边三角形；

②若AE=5，CE=2，求BF的长．

Answer 1

【答案】迁移应用：①证明见解析；②CD=AD+BD；拓展延伸：①证明见解析；②3.

【解析】

迁移应用：①如图②中，只要证明∠DAB=∠CAE，即可根据SAS解决问题；
②结论：CD=AD+BD．由△DAB≌△EAC，可知BD=CE，在Rt△ADH中，DH=ADcos30°=AD，由AD=AE，AH⊥DE，推出DH=HE，由CD=DE+EC=2DH+BD=AD+BD，即可解决问题；
拓展延伸：①如图3中，作BH⊥AE于H，连接BE．由BC=BE=BD=BA，FE=FC，推出A、D、E、C四点共圆，推出∠ADC=∠AEC=120°，推出∠FEC=60°，推出△EFC是等边三角形；
②由AE=5，EC=EF=2，推出AH=HE=2.5，FH=4.5，在Rt△BHF中，由∠BFH=30°，可得=cos30°，由此即可解决问题．

迁移应用：①证明：如图②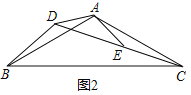

∵∠BAC=∠DAE=120°，
∴∠DAB=∠CAE，
在△DAE和△EAC中，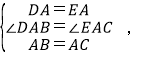
∴△DAB≌△EAC，

②解：结论：CD=AD+BD．
理由：如图2-1中，作AH⊥CD于H．

∵△DAB≌△EAC，
∴BD=CE，
在Rt△ADH中，DH=ADcos30°=AD，
∵AD=AE，AH⊥DE，
∴DH=HE，
∵CD=DE+EC=2DH+BD=AD+BD．
拓展延伸：①证明：如图3中，作BH⊥AE于H，连接BE．

∵四边形ABCD是菱形，∠ABC=120°，
∴△ABD，△BDC是等边三角形，
∴BA=BD=BC，
∵E、C关于BM对称，
∴BC=BE=BD=BA，FE=FC，
∴A、D、E、C四点共圆，
∴∠ADC=∠AEC=120°，
∴∠FEC=60°，
∴△EFC是等边三角形，

②解：∵AE=5，EC=EF=2，
∴AH=HE=2.5，FH=4.5，
在Rt△BHF中，∵∠BFH=30°，
∴=cos30°，
∴BF==3=3．