【题目】如图,![]() 是正方形
是正方形![]() 的对角线,点
的对角线,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 于点
于点![]() 交
交![]() 于点
于点![]() 连接
连接![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.

参考答案:
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)由正方形的性质,得到BC=CD,∠B=∠PCD=90°,由![]() ,则∠DEC=90°,利用等角的余角相等,得到∠BCQ=∠CDE,即可得到
,则∠DEC=90°,利用等角的余角相等,得到∠BCQ=∠CDE,即可得到![]() ;
;
(2)连接OB,由(1)可知BQ=CP,由正方形的性质得到∠OBQ=∠OCP=45°,OB=OC,然后得到△OBQ≌△OCP,即可得到OQ=OP.
证明:(1)∵四边形ABCD是正方形,
∴BC=CD,∠B=∠PCD=90°,
∵![]() ,
,
∴∠DEC=90°,
∴∠BQC+∠BCQ =90°,∠DCE+∠CDE=90°,
∵AB∥CD,
∴∠BQC=∠DCE,
∴∠BCQ=∠CDE,
∴![]() (ASA);
(ASA);
(2)如图,连接OB,

由(1)可知,![]() ,
,
∴BQ=CP,
∵四边形ABCD是正方形,
∴∠OBQ=∠OCP=45°,OB=OC,
∴△OBQ≌△OCP(SAS),
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,以点A为顶点的一个60°的角∠EAF绕点A旋转,∠EAF的两边分别交BC,CD于点E,F,且E,F不与B,C,D重合,连接EF.
(1)求证:BE=CF.
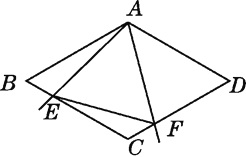
(2)在∠EAF绕点A旋转的过程中,四边形 AECF的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD交于点O,OE⊥AB,且OC平分∠AOE.
(1)如图1,求∠BOD的度数;
(2)如图2,过O点作射线OF,且∠DOF=4∠AOF,求∠FOC的度数.
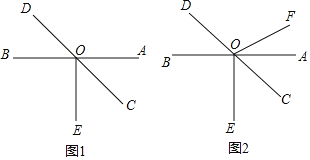
-
科目: 来源: 题型:
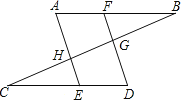
查看答案和解析>>【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.
-
科目: 来源: 题型:
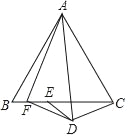
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
相关试题

