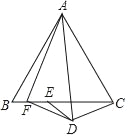
【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.
参考答案:
【答案】13![]() .
.
【解析】
作辅助线,构建直角三角形,先求CE的长,从而得FM和AM的长,根据勾股定理可得AF的长.
解:过D作DH⊥BC于H,
∵DC=DE=10,
∴EH=HC,
∵∠CDE=120°,
∴∠DCH=30°,
∴CH=EH=5![]() ,
,
∴CE=10![]() ,
,
∴BE=BC﹣CE=24﹣10![]() ,
,
∵F是BE的中点,
∴BF=![]() =12﹣5
=12﹣5![]() ,
,
过A作AM⊥BC于M,
∵△ABC是等边三角形,
∴BM=![]() BC=12,AM=12
BC=12,AM=12![]() ,
,
∴FM=BM﹣BF=12﹣(12﹣5![]() )=5
)=5![]() ,
,
由勾股定理得:AF=![]() =
=![]() =13
=13![]() .
.
故答案为:13![]() .
.
-
科目: 来源: 题型:
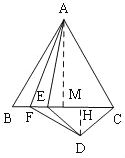
查看答案和解析>>【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是正方形
是正方形 的对角线,点
的对角线,点 是
是 的中点,点
的中点,点 是
是 上一点,连接
上一点,连接 于点
于点 交
交 于点
于点 连接
连接 .
.求证:(1)
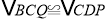 ;
;(2)
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
-
科目: 来源: 题型:
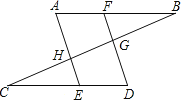
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
相关试题

